Synchronizace robotů
Zadání
Za námět úlohy vděčíme Jonathanu Weltonovi a jeho úloze Thunderball na stránkách http://www.mathpuzzle.com/26Mar03.html.
Obdélníková oblast je rozdělena na čtvercová pole a má M řádků a N sloupců. Na některých polích stojí roboti. Robotů je celkem K (1 ≤ K ≤ M×N) a na každém poli stojí nejvýše jeden. Roboti se pohybují v krocích a během svého pohybu každý robot označí každé pole, na které dorazí. V každém kroku se každý robot může posunout na pole bezprostředně sousední vlevo, vpravo, nahoře nebo dole a přitom toto pole nesmí být označené. Na začátku jsou označená pouze pole, na kterých jednotliví roboti stojí.
Roboti vykonávají jednotlivé kroky vždy současně na příkaz dispečera. Dispečer má k dispozici čtyři příkazy označené zkratkami L, H, P, D podle směru pohybu (doLeva, naHoru, doPrava, Dolu). Když dispečer vydá příkaz, každý z robotů se pokusí posunout o jedno pole ve směru daném v příkazu. Pokud je sousední pole v daném směru označené, to jest buď na něm stojí jiný robot nebo na něm kterýkoli z robotů již dříve stál, robot se neposune a zůstane stát. Robot se nemůže přesunout mimo danou obdélníkovou oblast, pokud stojí těsně u hranice oblasti a má se podle příkazu posunout v takovém směru, že by hranici překročil, také zůstane stát.
V oblasti je dále vyznačeno K tzv. cílových polí, na ně se mají roboti postupně přesunout tak, že po určitém počtu příkazů vydaných dispečerem bude každý robot stát na jednom cílovém poli. Nezáleží na tom, který robot bude stát na kterém cílovém poli.
Úloha
Na začátku je dán seznam polí, na kterých jednotliví roboti stojí před zahájením přesunu, a seznam cílových polí. Máme určit všechny takové co nejkratší posloupnosti příkazů dispečera, že po provedení kterékoliv z nich budou všichni roboti stát na cílových polích.
Poznámka: Když robot během svých přesunů dorazí na některé pole, ať už cílové nebo ne, a dispečer vydá další příkaz a robot může toto pole opustit, pak také robot toto pole opustí. Nicméně tím, že robot toto pole při svém příchodu označil, zároveň znemožnil další návrat kteréhokoli robota na toto pole. Proto, pokud robot opustí cílové pole, znemožní tak řešení úlohy.
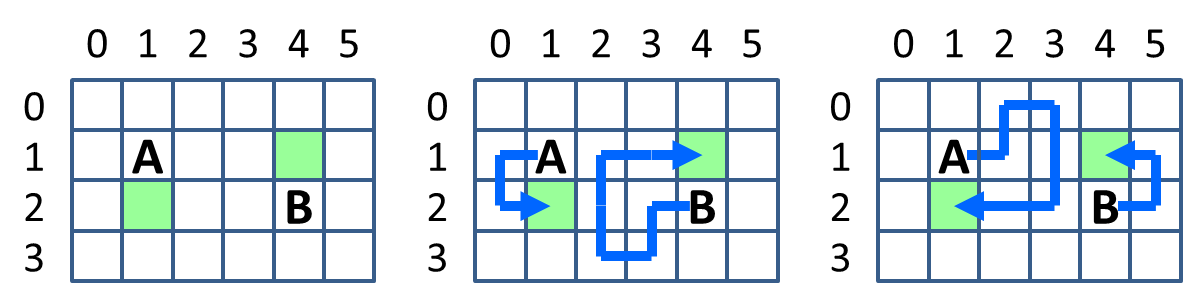
LDLHHPP, levý diagram znázorňuje přesun podle posloupnosti PHPDDLL.Vstup
Na vstupu jsou tři textové řádky. První řádek obsahuje čísla M, N, K v tomto pořadí oddělené mezerou. Druhý řádek obsahuje K celočíselných dvojic, každá dvojice obsahuje nejprve řádkovou a potom sloupcovou souřadnici jednoho robota. Třetí řádek obsahuje opět K celočíselných dvojic, každá dvojice obsahuje nejprve řádkovou a potom sloupcovou souřadnici jednoho cílového pole. Všechny hodnoty na řádku jsou odděleny mezerou, řádkové i sloupcové souřadnice se počítají od 0. Žádný robot nestojí na žádném z cílových polí.
Počet polí v oblasti nepřesáhne 50.
Výstup
Pokud neexistuje žádná posloupnost příkazů, pomocí níž se roboti mohou přesunout na cílová pole podle pravidel úlohy, výstup obsahuje jediný textový řádek s číslem 0.
Jinak výstup obsahuje jeden nebo více textových řádků, z nichž každý obsahuje jednu posloupnost příkazů, pomocí nichž se roboti mohou přesunout na cílová pole. Posloupnosti na výstupu jsou navzájem různé, nejkratší možné a všechny možné. Posloupnosti na výstupu jsou seřazeny v rostoucím lexikografickém pořadí, přičemž pro jednotlivé příkazy formálně platí L < H < P < D.
Počet posloupností na výstupu nepřesáhne 1000.
Příklady
Příklad 1
4 6 2
1 1 2 4
2 1 1 4LDLHHPP
PHPDDLLVstup a výstup popisuje situaci znázorněnou na Obr. 1 výše.
Příklad 2
4 4 4
0 0 0 3 3 0 3 3
1 1 1 2 2 1 2 2LPHD
LPDH
HDLP
HDPL
PLHD
PLDH
DHLP
DHPL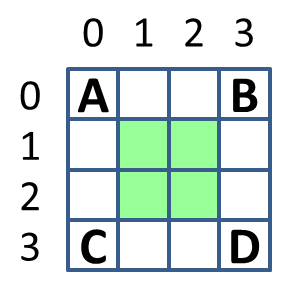
Příklad 3
3 7 3
1 3 2 6 2 1
1 6 1 1 0 0LHLHPPD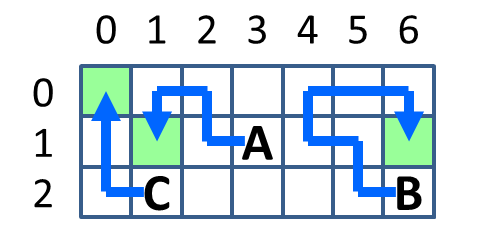
Veřejná data
Veřejná data k úloze jsou k dispozici. Veřejná data jsou uložena také v odevzdávacím systému a při každém odevzdání/spuštění úlohy dostává řešitel kompletní výstup na stdout a stderr ze svého programu pro každý soubor veřejných dat.