2. Rekurze

2 - Rekurze

Připomenutí teorie

Přednáška 2 v oddíle Přednášky

Rekurzivní funkce je ta, která volá sebe samu (přímo i nepřímo). Jednoduchým příkladem je například Fibonacciho posloupnost $f(N) = f(N-2) + f(N-1)$ . Jejich složitost lze často vyjádřit pomocí vzorce

T(n) = a T\left(\frac{n}{b}\right) + f(n)

kde $a$ je počet rekurzivních zavolání z jednoho průchodu funkce, $\frac{n}{b}$ je velikost vstupu pro dané podproblémy (vstup $n$ je rozdělen na $b$ stejných částí), a $f(n)$ je složitost jednoho průchodu funkce. Typicky složitost rozdělení dat a složení podvýsledků dohromady.

Složitost rekurzivních funkcí lze počítat různými způsoby.

Metodou rekurzivních stromů - rozkreselním stromu volání a sečtením složitosti.
Substituční metodou - Odhadem a následým ověřením skrze důkaz indukcí.
Mistrovskou větou (Master theorem) - Dosazením do vzorce a výpočtem.
- pokud $f(n) \in \mathrm{O}\left(n^{\log_b(a) - \epsilon}\right), \epsilon > 0$ , pak $T(n) \in \Theta \left(n^{\log_b(a)}\right)$ ,
- pokud $f(n) \in \Theta\left(n^{\log_b(a)}\right)$ , pak $T(n) \in \Theta\left(n^{\log_b(a)}\log(n)\right)$ ,
- pokud $f(n) \in \Omega\left(n^{\log_b(a) + \epsilon}\right), \epsilon > 0$ , a $a f\left(\frac{n}{b}\right) \leq c f(n), c < 1$ , pak $T(n) \in \Theta\left(f(n)\right)$ .

Jupyter notebook

Vybrané úlohy jsou připraveny v Jupyter notebooku.

Také na Google Colab.

Řešené úlohy

Úvod

Řešená úloha 1: Kolikrát bude zavolána funkce xyz() při zavolání rekur(5)?

void rekur(int x) {
  if(x < 1) return;
  rekur(x-1);
  xyz();
  rekur(x-2);
}

Řešení

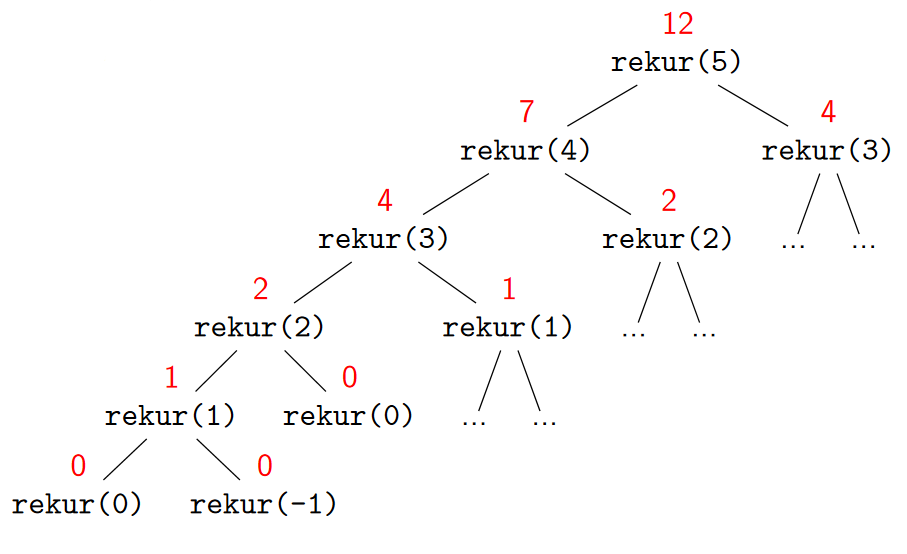
Solution

Řešená úloha 2: Charakterizujte slovy, jakou hodnotu vrátí funkce f(x, y) v závislosti na hodnotách jejích vstupních parametrů.

int f(int x, int y) {
  if(x > 0) return f(x - 1, y) + y;
  return 0;
}

Řešení

Vrátí $x \cdot y$ .

Řešená úloha 3: Napište rekurzivní funkci, která pro zadané číslo $N$ vypíše řetězec skládající se z $N$ jedniček následovaných $2N$ dvojkami. Pro dané $N$ bude funkce volat sama sebe právě $N$ -krát. Příklad: pro $N = 2$ vypíše 112222.

Řešení

def f(N):
    if N > 0:
        print(1)
        f(N - 1)
        print(2)
        print(2)

Řešená úloha 4: Rekurzivní algoritmus $\mathcal{A}$ dělí úlohu o velikosti $n$ na 2 stejné části. Každou část musí zpracovat dvakrát. Čas potřebný na rozdělení úlohy na části a na spojení dílčích řešení je úměrný hodnotě $n$ . Jak lze matematicky vyjádřit rekurentní vztah popisující složitost algoritmu $\mathcal{A}$ ?

Řešení

$T(n) = 4 T\left(\frac{n}{2}\right) + n$

Počítání složitosti

Řešená úloha 5: Rekurzivní algoritmus $\mathcal{A}$ pracuje tak, že pro $n > 1$ data rozdělí na $4$ části stejné velikosti, zpracuje $5$ těchto částí (tj. jednu dvakrát), a pak jejich řešení spojí. Na samotné rozdělení problému a spojení řešení menších částí potřebuje dobu úměrnou $n^2–n$ .

Určete asymptotickou složitost pomocí

stromu rekurze,
Mistrovské věty,
a substituční metody.

Strom rekurze

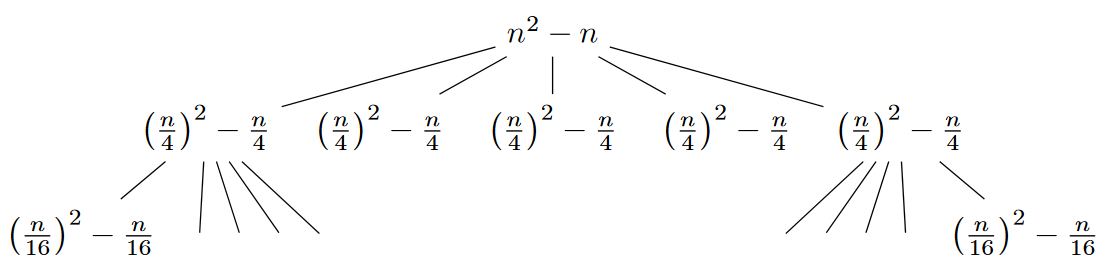
Solution

V $i$ -té úrovni je $5^i$ uzlů, protože v každé úrovni se počet uzlů zvětší $5$ -krát.
V jednom uzlu v hloubce $i$ proběhne $\left(\frac{n}{4^i}\right)^2 - \frac{n}{4^i}$ operací, protože v $i$ -té úrovni jsme problém zmenšili $4^i$ -krát.
Hloubka stromu je $\log_4(n)$ , protože v každé úrovni dělíme problém na čtvrtiny, a $\frac{n}{4^i} = 1$ pro $i = \log_4 n$ .
Nejhlubší úroveň má konstantní složitost v každém uzlu, $5^{\log_4(n)} = n^{\log_4(5)}$ uzlů. Tedy $\Theta\left(n^{\log_4(5)}\right)$ .
Hloubka $i$ vyžaduje $5^i \left[ \left(\frac{n}{4^i} \right)^2 - \frac{n}{4^i}\right] = n^2 \left(\frac{5}{16}\right)^i - n \left(\frac{5}{4}\right)^i, 0 \leq i \leq d - 1$ operací.
- Celkem tedy:
  
  $\sum_{i=0}^{\log_4 n-1} n^2 \left(\frac{5}{16}\right)^i - n \left(\frac{5}{4}\right)^i = n^2 \sum_{i=0}^{\log_4 n - 1} \left(\frac{5}{16}\right)^{i} - n \sum_{i=0}^{\log_4 n - 1}\left(\frac{5}{4}\right)^{i}$
- Což jsou součty 2 geometrických posloupností. Vzorec pro součet prvků geoemetrické posloupnosti je nám známý: $\sum_{i=0}^{k-1} a_1q^{i} = a_1\frac{q^k - 1}{q - 1}, q \neq 1$ .
Celková složitost je

\begin{align*} &\Theta\left(n^2 \frac{1-\left(\frac{5}{16}\right)^{\log_4 n}}{1 - \frac{5}{16}} - n \frac{1-\left(\frac{5}{4}\right)^{\log_4 n}}{1-\frac{5}{4}} + n^{\log_4 5}\right) \\\ = &\Theta\left(\frac{16n^2}{11}\left(1-n^{\log_4\frac{5}{16}}\right) + 4n \left(1-n^{\log_4\frac{5}{4}}\right) + n^{\log_4 5}\right) \\\ = &\Theta\left(\frac{16}{11}n^2 - \frac{16}{11}n^{\log_4 5} + 4n - 4n^{\log_4 5} + n^{\log_4 5}\right) \\\ = &\Theta\left(n^2 + n - n^{\log_4 5}\right) = \Theta\left( n^2\right) \end{align*}

Mistrovská věta

Ze zadání máme $T(n) = 5T\left(\frac{n}{4}\right) + (n^2 - n)$ , tedy $a=5$ , $b=4$ a $f(n) = n^2 - n$ . Z hrubého porovnání $f(n)$ a $n^{\log_b(a)}$ , tedy $\Theta(n^2)$ a $n^{\log_4 5}$ odhadneme, že by mohlo jít o 3. možnost.

Existuje takové $\epsilon > 0$ , aby $(n^2-n) \in \Omega\left(n^{\log_4(5) + \epsilon}\right)$ ? Pro $\epsilon = 2 - \log_4(5)$ dostáváme $(n^2 - n) \in \Omega\left(n^2\right)$ , což jistě platí, protože $(n^2 - n) \in \Theta(n^2)$ .

Existuje takové $c<1$ , aby $5 \left(\frac{n^2}{16} - \frac{n}{4}\right) \leq c (n^2 - n)$ ? Ano, například $c=5/16$ .

Takže $T(n) \in \Theta(n^2 - n) = \Theta(n^2)$

Substituční metoda

Chceme ukázat, že $T(n) \in O(n^2)$ , kde $T(n) = 5T\left(\frac{n}{4}\right) + (n^2 - n)$ . Tedy z definice: $T(n) \leq c n^2$ pro nějaké $c > 0$ a $n_0 > 0$ .

Přecházíme k indukci:

Předpokládáme, že platí $T\left(\frac{n}{4}\right) \leq c \left(\frac{n}{4}\right)^2$ a chceme ukázat $T(n) \leq c n^2$
- $T(n) = 5 T\left(\frac{n}{4}\right) + (n^2 - n)$
- $T(n) \leq 5 c\left( \frac{n}{4} \right)^2 + (n^2 - n)$ (z indukčního předpokladu)
- $T(n) \leq n^2(\frac{5c}{16} + 1) - n \leq cn^2$ což platí např. pro $c = 16$ .

Zbývá najít $n_0$ :

\begin{align*} T(n) = n^2(\frac{5 \cdot 16}{16} + 1) - n &\leq 16 \cdot n^2 \\\ 6 n^2 - n &\leq 16 n^2, \end{align*}

což platí i pro $n_0 = 1$

Dokázali jsme $T(n) \in O(n^2)$ . Pro $T(n) \in \Omega(n^2)$ bychom postupovali obdobně, a z toho že $T(n) \in O(n^2) \cap \Omega(n^2)$ získáme $T(n) \in \Theta(n^2)$

Další úlohy

Úloha 6: Určete, jakou hodnotu vypíše program po vykonání příkazu print(rekur(4));

int rekur(int x) {
  if (x < 1) return 2;
  return (rekur(x-1) + rekur(x-1));
}

Co tato funkce počítá?

Úloha 7: Uvažujte podobnou funkci jako ve cvičení 2. Doplňte prázdná místa tak, aby vracela $x^y$ .

int f(int x, int y) {
  if(____) return ____;
  return ____;
}

Úloha 8: Daná funkce ff je volána takto: ff(a, b);, a i b jsou celá kladná čísla. Napište vztah, který určí, kolikrát bude volána funkce abc(x), v závislosti na hodnotě parametrů a, b.

void ff(int x, int p) {
  if (x > 0) ff(x–p, p);
  abc(x);
  if (x > 0) ff(x–p, p);
}

Úloha 9: Pomocí rekurzivní funkce vypište pro zadané kladné číslo N posloupnost čísel:

1 2 … N−2 N−1 N N N−1 N−2 … 2 1

Úloha 10: Rekurzivní algoritmus $\mathcal{A}$ dělí úlohu o velikosti $n$ na 3 stejné části a pro zisk výsledku stačí, když zpracuje pouze dvě z nich. Čas potřebný na rozdělení úlohy na části a na spojení dílčích řešení je úměrný hodnotě $n^2$ . Zapište rekurentní vztah pro asymptotickou složitost algoritmu $\mathcal{A}$ .

⭐ Úloha 11: Daný rekurzivní algoritmus pracuje tak, že pro $n > 1$ data rozdělí na $3$ části stejné velikosti, zpracuje každou tuto část dvakrát a pak jejich řešení spojí. Na samotné rozdělení problému a spojení řešení menších částí potřebuje dobu úměrnou hodnotě $n^{1/2} \cdot \log_2(n)$ . Jakou má daný algoritmus asymptotickou složitost?

Řešte pomocí Vaší oblíbené metody.

⭐ Úloha 12: Uvažme následující algoritmus pro řazení pole délky n.

Seřaď levou polovinu pole (rekurzivním voláním).
Seřaď pravou polovinu pole (rekurzivním voláním).
Zkombinuj výsledky do seřazeného pole.

Jaká je asyptotická složitost tohoto algoritmu, pokud přepokládáme, že jsme schopni výsledky zkombinovat v $\Theta(n)$ ? A co v případě, že to zkombinování má složitost $\Theta(n^2)$ ?

Úloha 13: Složitost rekurzivního algoritmu je dána rekurencí:

a) $T(n) = 3 \cdot T(\lfloor n/2 \rfloor) + n$
b) $T(n) = T(n/2) + n^2$
c) $T(n) = 4 \cdot T(n/2 + 2) + n$
Použijte metodu stromu rekurze k nalezení vhodného (těsného) horního asymmptotického odhadu funkce $T(n)$ .

Ověřte výsledek substituční metodou.

⭐ Úloha 14: Složitost rekurzivního algoritmu je dána rekurencí:

a) $T(n) = T(n−1) + T(n/2) + n$
b) $T(n) = T(n−a) + T(a) + cn$ , kde $a \ge 1, c \> 0$
c) $T(n) = T(\alpha n) + T((1 − \alpha)n) + cn$ , kde $0 < \alpha < 1, c > 0$ .
Použijte metodu stromu rekurze k nalezení vhodného horního odhadu funkce $T(n)$ .

Úloha 15: Pro složitost rekurzivního algoritmu platí T(1) = 1. Pro každé n > 1 je T(n) dána rekurencí:

a) $T(n) = \sum_{k=1}^{n-1} T(k) + 1$
b) $T(n) = \sum_{k=1}^{n-1} T(k) + 7$
c) $T(n) = \sum_{k=1}^{n-1} T(k) + n^2$
d) $T(n) = 2\sum_{k=1}^{n-1} T(k) + 1$

Určete řád růstu funkce $T(n)$ .

Úloha 16: Sierpińského koberce

Prvky pole $P_N$ o velikosti $3^N \times 3^N$ jsou pouze čísla $1$ a $0$ . Obrázky níže znázorňují pole $P_N$ pro několik hodnot $N$ , modrá barva představuje hodnotu $1$ , bílá $0$ . Napište kód, který pro dané $N$ vytvoří a vyplní pole $P$ podle daného vzoru.

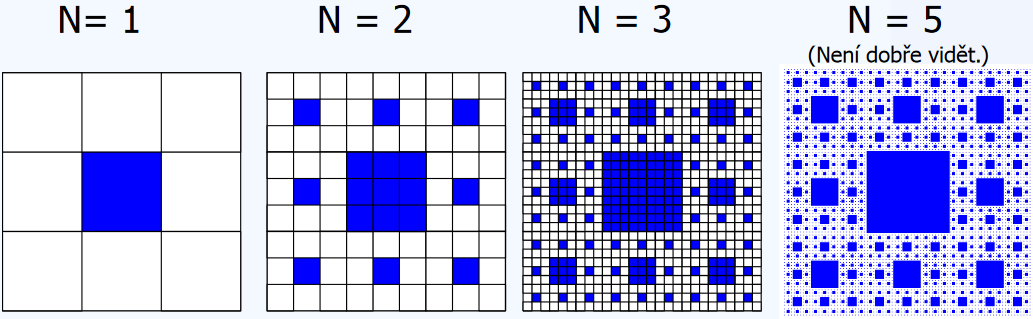
Úloha 17: Seznamte se s Ackermanovou funkcí.

\begin{equation*}A(n, m) = \begin{cases} m + 1 & n = 0 \\\ A(n-1, 1) & n > 0, m = 0 \\\ A(n-1, A(n, m-1)) & n > 0, m > 0 \\\ \end{cases} \end{equation*}

Zkuste spočítat hodnotu $A(4, 4)$ .

⭐ Úloha 18: Násobení matic

Nechť $X$ a $Y$ jsou matice tvaru $n \times n$ , kde n je přirozené číslo. Uvažujme násobení matic $Z = X \cdot Y$ podle definice pro násobení matic, tedy: $z_{ij} = \sum_{k=1}^{n} x_{ik} \cdot y_{kj}$ .

Jaká je složitost výpočtu podle této definice?

Nyní uvažujme násobení matic pomocí rekurze. Pro jednoduchost předpokládejme, že n je mocninou dvou. Pak můžeme matice násobit po blocích. Představme, si že matice $X$ a $Y$ rozdělíme na 4 stejně velké podmatice:

$X = \begin{bmatrix} A & B \\ C & D \end{bmatrix}$

$Y = \begin{bmatrix} E & F \\ G & H \end{bmatrix}$

Pak můžeme využít vztahu:

$X \cdot Y = \begin{bmatrix} {AE + BG} & {AF + BH} \\ {CE + DG} & {CF + DH} \end{bmatrix}$ .

Jaká je asymptotická složitost takového rekurzivního algoritmu?

Jaká je asymptotická složitost Strassenova algoritmu, pro který platí:

$X \cdot Y = \begin{bmatrix} {T_5 + T_4 - T_2 + T_6} & {T_1 + T_2} \\ {T_3 + T_4} & {T_1 + T_5 - T_3 - T_7} \end{bmatrix}$ ,

kde:

$T_1 = A(F - H)$
$T_2 = (A + B)H$
$T_3 = (C + D)E$
$T_4 = D(G - E)$
$T_5 = (A + D)(E + H)$
$T_6 = (B - D)(G + H)$
$T_7 = (A - C)(E + F)$ ?