3 - Binární stromy
Připomenutí teorie
Přednáška 3 v oddíle Přednášky.
Stromy jsou hierarchická datová struktura. Mohou být binární, ternární, n-ární…
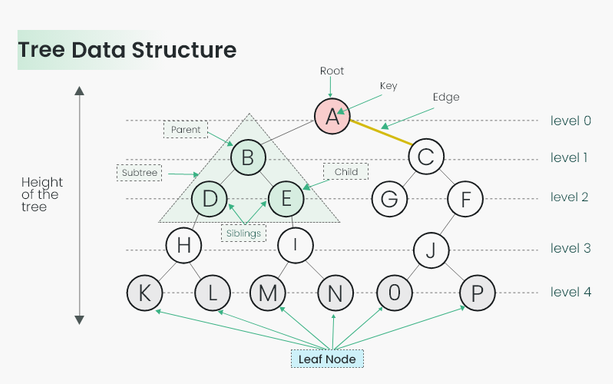
Obrázek z Geeks for geeks.
-
Hloubka je počet hran na cestě z kořene.
-
Výška je počet hran na cestě do nejvzdálenějšího listu.
Dále existuje Předek (Ancestor), což je uzel, který je od rodiče dál směrem ke kořeni.
Uzel, který není list, se nazývá vnitřní (inner), a říká se, že se “větví” na potomky. Podstrom každého potomku je pak větev (branch).
| English | Česky |
|---|---|
Node (Vertex) |
Uzel |
Key |
Klíč (Hodnota v uzlu) |
Edge |
Hrana |
Root |
Kořen |
Leaf |
List |
Height |
Výška (stromu) |
Depth |
Hloubka (uzlu) |
Level |
Úroveň (Patro) |
Parent |
Rodič |
Child |
Potomek |
Siblings |
Sourozenci |
Subtree |
Podstrom |
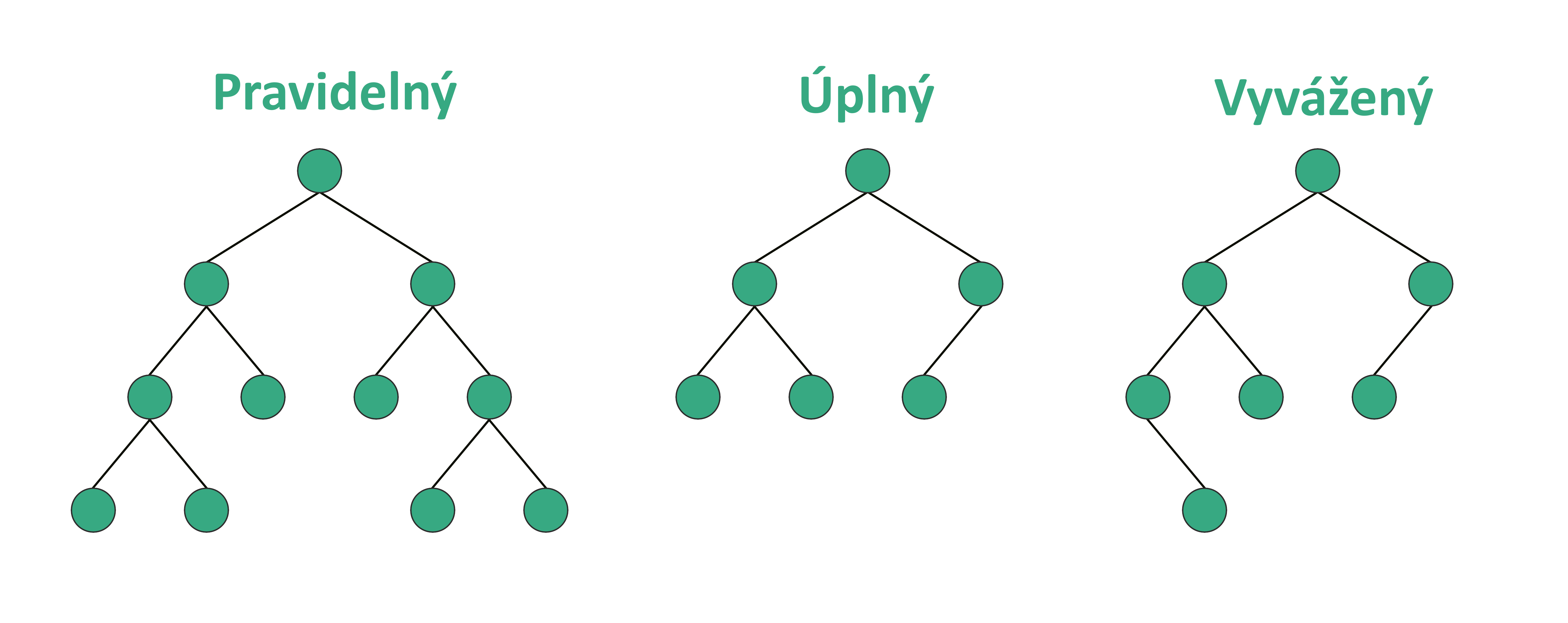
Typy
Binární strom může být:
-
Pravidelný (Regular): Každý uzel má buď nula nebo dva potomky.
-
Úplný (Complete): Strom má všechny listy v nejhlubší úrovni (Pokud není vhodný počet uzlů, poslední úroveň má přebytek listů zleva)
-
Vyvážený (Balanced): Rozdíl hloubek podstromů pro každé sourozence musí být maximálně roven jedné.
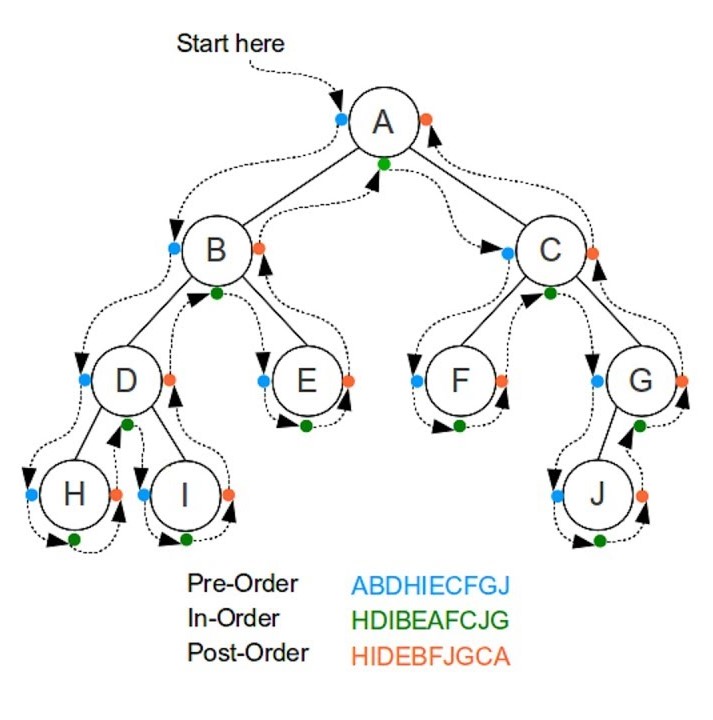
Průchody
struct TreeNode{
int val;
TreeNode* left, right;
};
void traversal(TreeNode* node) {
if (node){
cout << node->val << " "; // pre-order
traversal(node->left); // levý podstrom
cout << node->val << " "; // in-order
traversal(node->right); // pravý podstrom
cout << node->val << " "; // post-order
}
}Vizualizace průchodů na Geeks for geeks.
Řešené úlohy
Řešená úloha 1: Jaká je minimální možná hloubka binárního stromu s 300 listy? Jak bude takový strom vypadat?
Řešení
Půjde o úplný binární strom. V poslední úrovni bude listů. Takže
Co když bude strom ternární?
Řešená úloha 2: Pravidelný binární strom má uzlů. Kolik má listů?
Řešení
Listů má což lze dokázat pomocí indukce.
Intuitivně, pravidelný strom má lichý počet uzlů, přidání uzlů je možné jen po dvou, což změní celkový počet listů o jeden.
Řešená úloha 3: Daný binární strom má tři listy. Tudíž:
a) má nejvýše dva vnitřní uzly
b) počet vnitřních uzlů není omezen
c) všechny listy mají stejnou hloubku
d) všechny listy nemohou mít stejnou hloubku
e) strom je pravidelný
Řešení
Pouze b) je správně. Protipříklady:
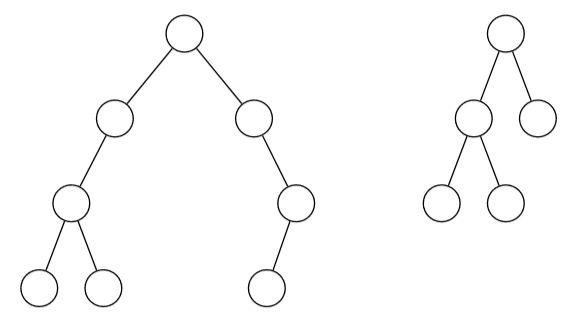
Řešená úloha 4:
Určete posloupnost zpracovaných uzlů daného stromu (napravo) při průchodu v pořadí
-
Pre-order
-
In-order
-
Post-order
Pre-order
B, O, H, M, R, L, K, J, A, E, D, V
In-order
M, H, R, O, K, L, B, A, E, J, V, D
Post-order
M, R, H, K, L, O, E, A, V, D, J, B
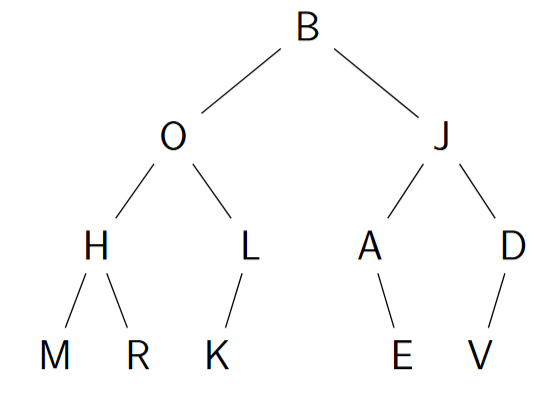
Řešená úloha 5: Algoritmus provádí průchod v pořadí in-order binárním vyváženým stromem s uzly a v každém uzlu provádí navíc další (nám neznámou) akci, jejíž složitost je . Jaká je asymptotická složitost ?
Řešení
, protože průchod stromem má lineární složitost vůči počtu uzlů.
Další úlohy
Úloha 6: Jaká je maximální možná hloubka binárního stromu s 300 listy?
Úloha 7: Algoritmus provede jeden průchod binárním stromem s hloubkou . Při zpracování celé -té úrovně (= všech uzlů s hloubkou ) provede operací. Jaká je asymptotická složitost ? Vyjádřete ji jako funkci proměnné .
⭐ Úloha 8: Máme projít pravidelným binárním stromem a navštívit všech jeho uzlů. Jediné dvě možnosti pohybu v každém uzlu jsou buď posun do některého bezprostředního potomka nebo skok zpět do kořene stromu. Každý posun nebo skok trvá jednu mikrosekundu.
Za jak dlouho lze úkol splnit, pokud
a) strom má minimální možnou hloubku,
b) strom má maximální možnou hloubku?
Bonus: Strom s kolika uzly zvládne algoritmus zpracovat za jednu sekundu?
Konstrukční úlohy
Úloha 9: Popište tvar binárního stromu, pro nějž platí:
-
Průchod v pořadí Inorder a Preorder vytvoří stejnou posloupnost uzlů.
-
Průchod v pořadí Inorder a Postorder vytvoří stejnou posloupnost uzlů.
-
Průchod v pořadí Preorder a Postorder vytvoří stejnou posloupnost uzlů.
-
Průchod v pořadí Inorder a Preorder a Postorder vytvoří stejnou posloupnost uzlů.
⭐ Úloha 10: Při průchodu stromem v pořadí Inorder a Preorder získáme následující posloupnosti klíčů uložených v jeho jednotlivých (celkem devíti) uzlech:
Inorder |
45 |
71 |
98 |
47 |
50 |
62 |
87 |
3 |
79 |
Preorder |
50 |
47 |
71 |
45 |
98 |
62 |
3 |
87 |
79 |
Rekonstruujte tvar stromu.
Bonus: Navrhněte a formulujte algoritmus, který zkonstruuje libovolný strom z jeho Inorder a Preorder posloupností.
⭐ Úloha 11: Navrhněte algoritmus, který pro danou vstupní hodnotu vytvoří binární strom s uzly jehož hloubka nebude vyjádřena výrazem ani ani , ale výrazem .
Implementační úlohy
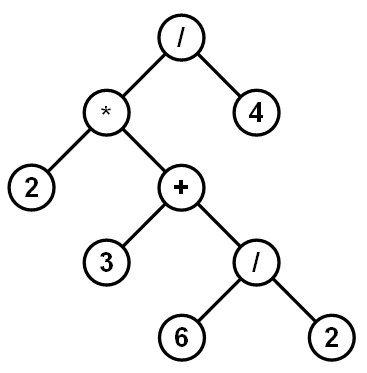
Úloha 12: Napište pseudokód funkce, která z binárního stromu odstraní všechny listy.
Úloha 13: Napište pseudokód funkce, která každému uzlu v binárním stromu přiřadí hodnotu jeho výšky. (Neboli výšky stromu který obsahuje všechny potomky daného uzlu)
Úloha 14: Napište pseudokód funkce, která vytvoří přesnou kopii binárního stromu.
Úloha 15: Napište pseudokód funkce, která daný binární strom modifikuje tak, že výsledný strom bude zrcadlovým obrazem původního.
Musí platit, že výpis uzlů původního stromu v pořadí Inorder vytvoří opačně uspořádanou posloupnost než výpis uzlů modifikovaného stromu taktéž v pořadí Inorder.
Úloha 16: Aritmetický výraz obsahující celá čísla, závorky a operace (celočíselné dělení) může být reprezentován jako pravidelný binární strom. Popište, jak takový strom obecně vypadá, navrhněte implementaci uzlu a napište funkci, jejímž vstupem bude ukazatel na kořen stromu a výstupem hodnota odpovídajícího aritmetického výrazu.