4. Prohledávání grafu

4 - Prohledávání grafu

Připomenutí teorie

Přednáška 4 v oddíle Přednášky.

Graf je zobecněním stromu. Názvosloví z většiny zůstává, jen nelze hovořit o předcích a potomcích, protože obecný graf nemá kořen a může obsahovat cykly, nebo být nesouvislý (Strom je definován jako acyklický souvislý graf). Uzly spojené hranou se nazývají sousedé (neighbors).

Prohledávání stromu lze zapsat takto:

    function search(data_structure):
      while data_structure is not empty
        take node from data_structure
        process node
        add children of node to data_structure

V případě obecného grafu musíme kontrolovat abychom nenavštěvovali uzly vícekrát - přidáváme pouze sousedy, které jsme ještě nepřidali. Za tím účelem si ukládáme seznam viděných uzlů.

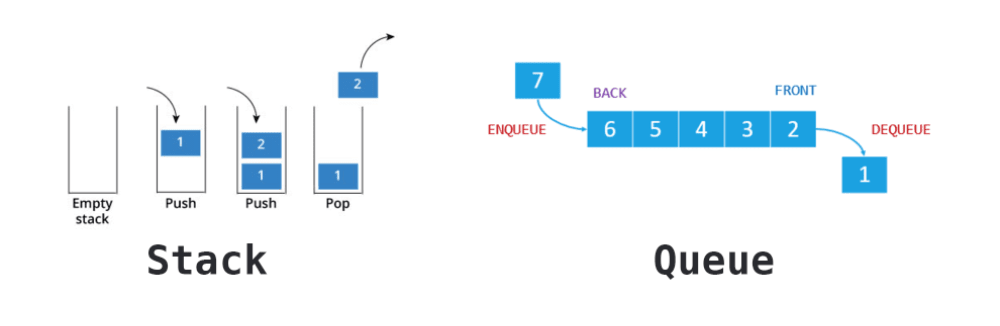
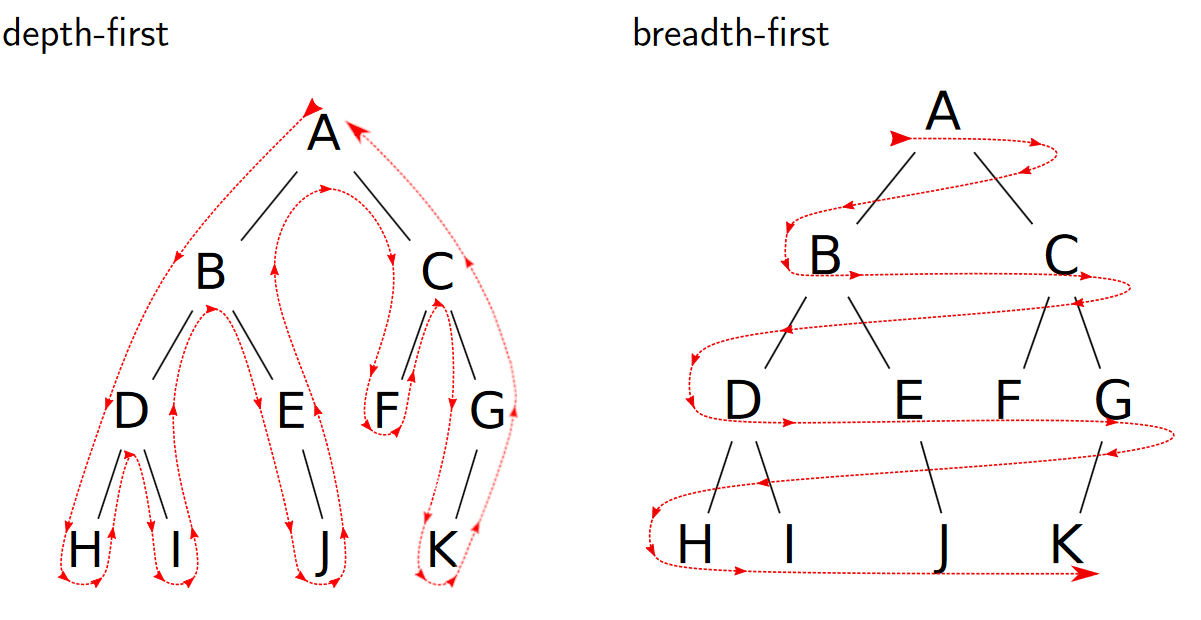
Na základě toho, zda je data_structure zásobník (stack) či fronta (queue) pak algoritmus provádí DFS či BFS.

Prohledávání

Do hloubky - Depth-first search (DFS)

Využívá zásobník (stack), což je last-in first-out (LIFO) datová struktura. To znamená, že při odebrání prvku ze zásobníku vezmeme prvek, co byl přidán naposledy.

Do šířky - Breadth-first search (BFS)

Využívá frontu (queue), což je first-in first-out (FIFO) datová struktura. To znamená, že při odebrání prvku z fronty vezmeme prvek, co byl přidán první, tedy ten co je ve frontě “nejdéle”.

Video vizualizace

Řešené úlohy

Fronta & Zásobník

Řešená úloha 1: Co bude obsahovat ds po každém řádku a co vypíše následující program pokud ds je zásobník? A co v případě, že je ds fronta?

ds.push(1)
ds.push(2)
print(ds.pop())
print(ds.peek())
print(ds.peek())
ds.push(3)
print(ds.pop())
print(ds.pop())
print(ds.peek())
ds.push(4)
ds.push(5)
print(ds.pop())
print(ds.pop())

Řešení

Zásobník: 2, 1, 1, 3, 1, null, 5, 4
Fronta: 1, 2, 2, 2, 3, null, 4, 5

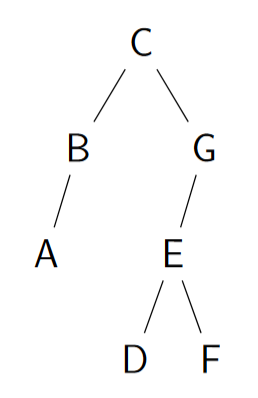
Řešená úloha 2:

Strom na obrázku procházíme do šířky. V určitém okamžiku jsou ve frontě uzly (uzly jsou přidávány podle abecedy, konec fronty je vpravo):

Řešení

b) a f)

Stromy

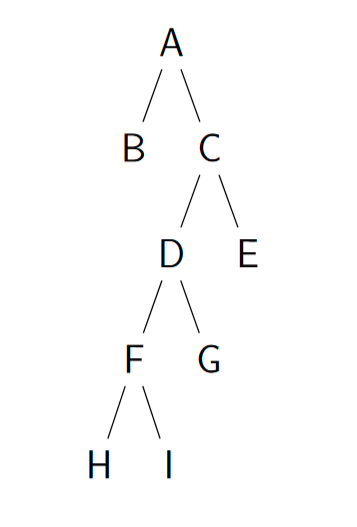
Řešená úloha 3: Rekonstruujte strom z následujících průběžných obsahů fronty při prohledávání do šířky:

Řešení

Obecné grafy

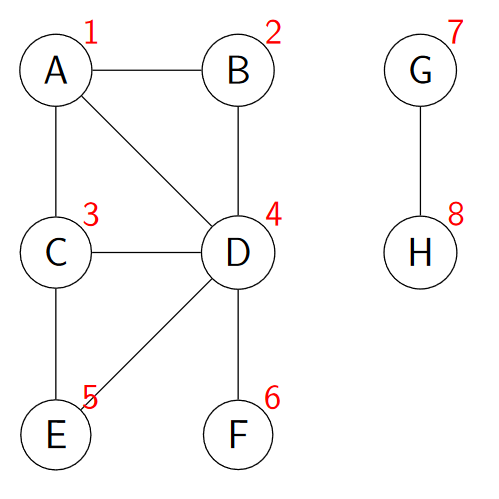
Řešená úloha 4: Uvažujte následující graf. Následníky zpracovávejte v abecedním pořadí.

graph

Očíslujte vrcholy podle otevíracích při průchodu do šířky.

Řešení BFS

bfs

Očíslujte vrcholy podle otevíracích a zavíracích časů při průchodu do hloubky.

Řešení DFS

dfs

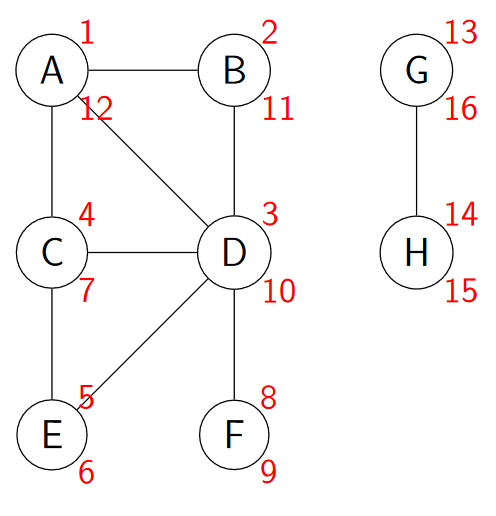
Další úlohy

⭐ Úloha 5: Najděte (libovolnou) cestu z uzlu E do uzlu A a spočítejte její celkovou cenu. Jaký algoritmus nalezne cestu, obsahující nejméně hran? Jak algoritmicky naleznete cestu s nejmenším součtem cen hran?

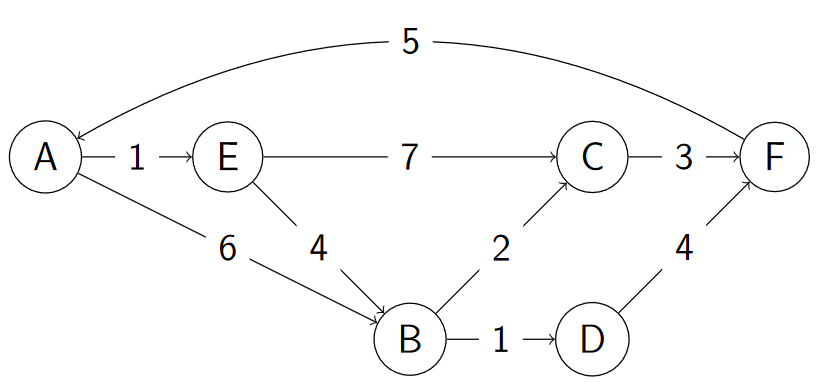
hint: Dijkstra

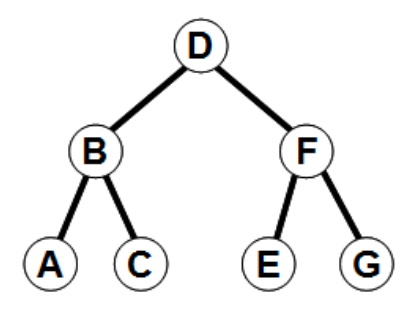
Úloha 6:

Strom na obrázku procházíme do šířky. V určitém okamžku jsou ve frontě následující uzly (čelo fronty je vlevo).

D
DF
FB
BGE
BAC
ABCD

Úloha 7: Formulujte obecný algoritmus, jak z dané posloupnosti obsahů fronty (jako v úloze 3) rekonstruovat pravidelný strom.

Grafy v praxi

Následující úlohy jsou k dispozici také v Jupyter notebooku nebo na Google Colab.

A jejich řešení jsou k dispozici v Jupyter notebooku nebo na Google Colab.

💻Úloha 8: Máte sedm kamenů a šest žab. Výchozí pozice zelených a hnědých žab jsou odděleně na opačných koncích rybníčku. Jediný volný kámen je tedy uprostřed. Vaším úkolem je pak postupně přemístit žáby do výchozích pozic jejich jinobarevných kolegyň.

Počáteční stav initial state

Konečný stav final state

Pohyb žáby je možný pouze skokem na volný kámen před její pozicí nebo přeskokem přes jednu žábu (libovolné barvy) na volnou pozici za ní. Skok zpět žába nemá dovoleno, takže musíte všechny skoky pečlivě naplánovat.

Použijte prohledávání stavového prostoru řešení.

Simulace

💻Úloha 9: Hanojské věže

Hlavolam se skládá ze tří kolíků (věží). Na začátku je na jednom z nich nasazeno několik kotoučů různých poloměrů, seřazených od největšího (vespod) po nejmenší (nahoře). Úkolem řešitele je přemístit všechny kotouče na druhou věž (třetí přitom využije jako pomocnou pro dočasné odkládání) podle následujících pravidel:

V jednom tahu lze přemístit jen jeden kotouč.
Jeden tah sestává z vzetí vrchního kotouče z některé věže a jeho položení na vrchol jiné věže.
Je zakázáno položit větší kotouč na menší.

Použijte prohledávání stavového prostoru řešení.

Simulace

💻Úloha 10: Tři misionáři se vydali na osvětovou misii a jako průvodce mají tři kanibaly. Potřebují překonat řeku, ovšem loďka uveze nejvýše dva lidi. Kanibalové zatím nejsou dostatečně poznamenáni misionářskou osvětou, takže pokud se kdykoli vyskytne na jednom místě více kanibalů než misionářů, budou misionáři snězeni. Jinak však kanibalové spolupracují a udělají, co jim misionáři řeknou. Jak se může celá skupina dostat na druhý břeh?

Použijte prohledávání stavového prostoru řešení.

Simulace

💻Úloha 11: Máme 3 nádoby o různých objemech. Žádná nádoba na sobě nemá stupnici a nádoby mají dokonce tak roztodivné tvary, že nám znemožňují odhadování množství vody v nich. Stále ale může naměřit i jiné množství tekutiny. Můžeme přelévat obsah jedné nádoby do druhé tak dlouho, dokud nepřelijeme všechno nebo dokud se druhá nádoba nezaplní. Jaký je nejmenší počet přelití, abychom vyřešili následující úlohy? Ve všech variantách je na počátku největší nádoba plná.

Máme 3 nádoby o objemech 7l, 5l a 3l. Chceme naměřit 1 litr.
Máme 3 nádoby o objemech 7l, 4l a 3l. Přeléváním se chceme dostat do stavu, kdy je v jedné nádobě 3l a ve zbylých dvou po 2 litrech.
Máme 3 nádoby o objemech 8l, 5l a 3l. Přeléváním se chceme dostat do stavu, kdy je počáteční množství rozděleno na dva stejné díly.

Použijte prohledávání stavového prostoru řešení.

💻Úloha 12: Zkuste využít BFS nebo DFS na úlohu Safe Passage. Cílem je najít nerychlejší způsob jak projít kolem stráže když máme plášť neviditelnosti, pod který se vejdou jen 2 lidé najednou.