6. AVL + B-strom

6 - AVL + B-strom

Připomenutí teorie

Přednáška 6 v oddíle Přednášky.

AVL

Název je podle autorů (Adelson-Velsky a Landis), nemá význam. AVL udržuje vyváženost stromu a tak zajišťuje logaritmickou složitost operací. Potřeba vyvažovat se zjišťuje z rozdílu hloubek podstromů daného uzlu. Pokud je větší než 1, provádíme rotaci:

Jednoduché rotace - když je větší hloubka na stejné straně (uzel i jeho potomek na hlubší straně mají hlubší podstrom na stejné straně), nebo mají oba podstromy na hlubší straně stejnou hloubku.
- R rotace - rotace doprava - levý podstrom je o 2 hlubší než pravý podstrom, a kořen levého podstromu (levý potomek) má taktéž hlubší podstrom u levého potomka, nebo jsou oba jeho podstromy stejně hluboké
- L rotace - rotace doleva - pravý podstrom je o 2 hlubší než levý podstrom, a kořen pravého podstromu (pravý potomek) má taktéž hlubší podstrom u pravého potomka, nebo jsou oba jeho podstromy stejně hluboké

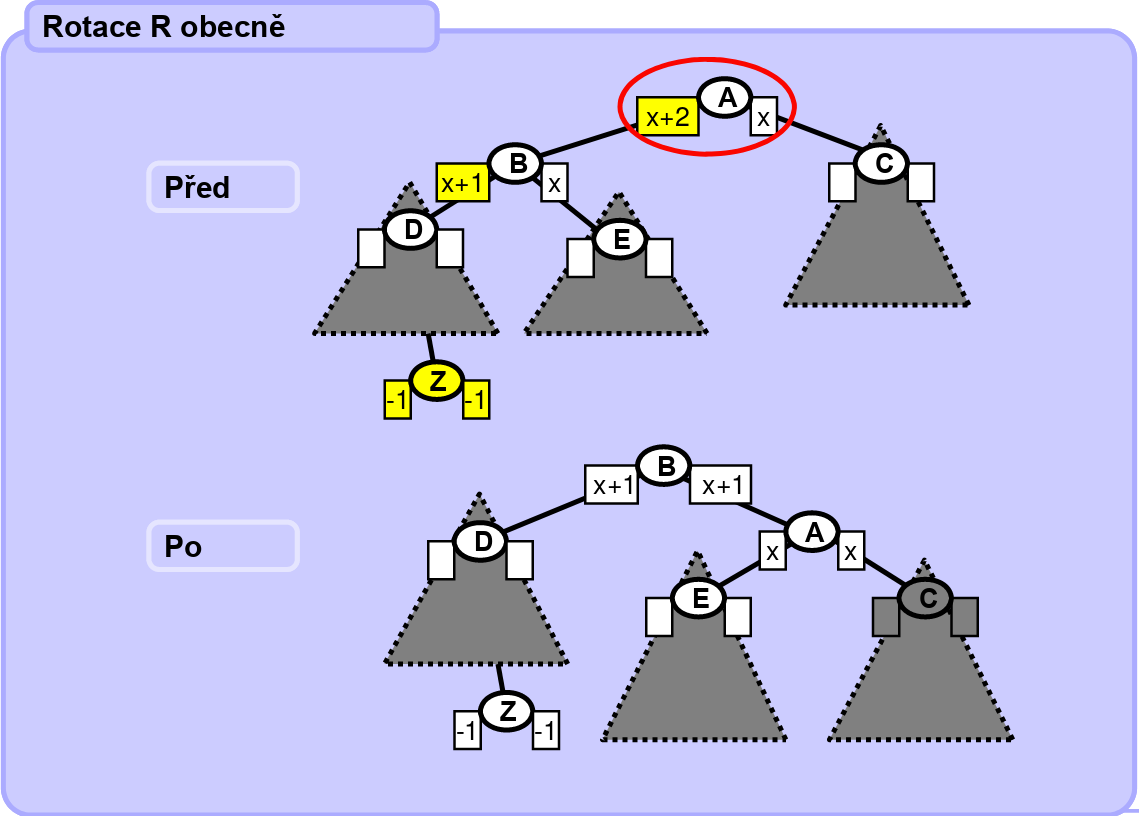
rotace_r

rotace_l

Dvojité rotace - když je větší hloubka na jiné straně (uzel a jeho potomek na hlubší straně mají hlubší podstrom na různých stranách)
- LR rotace - L rotace v levém potomkovi a pak R rotace - levý podstrom je o 2 hlubší než pravý podstrom, a kořen levého podstromu (levý potomek) má hlubší podstrom u pravého potomka
- RL rotace - R rotace v pravém potomkovi a pak L rotace - pravý podstrom je o 2 hlubší než levý podstrom, a kořen pravého podstromu (pravý potomek) má hlubší podstrom u levého potomka

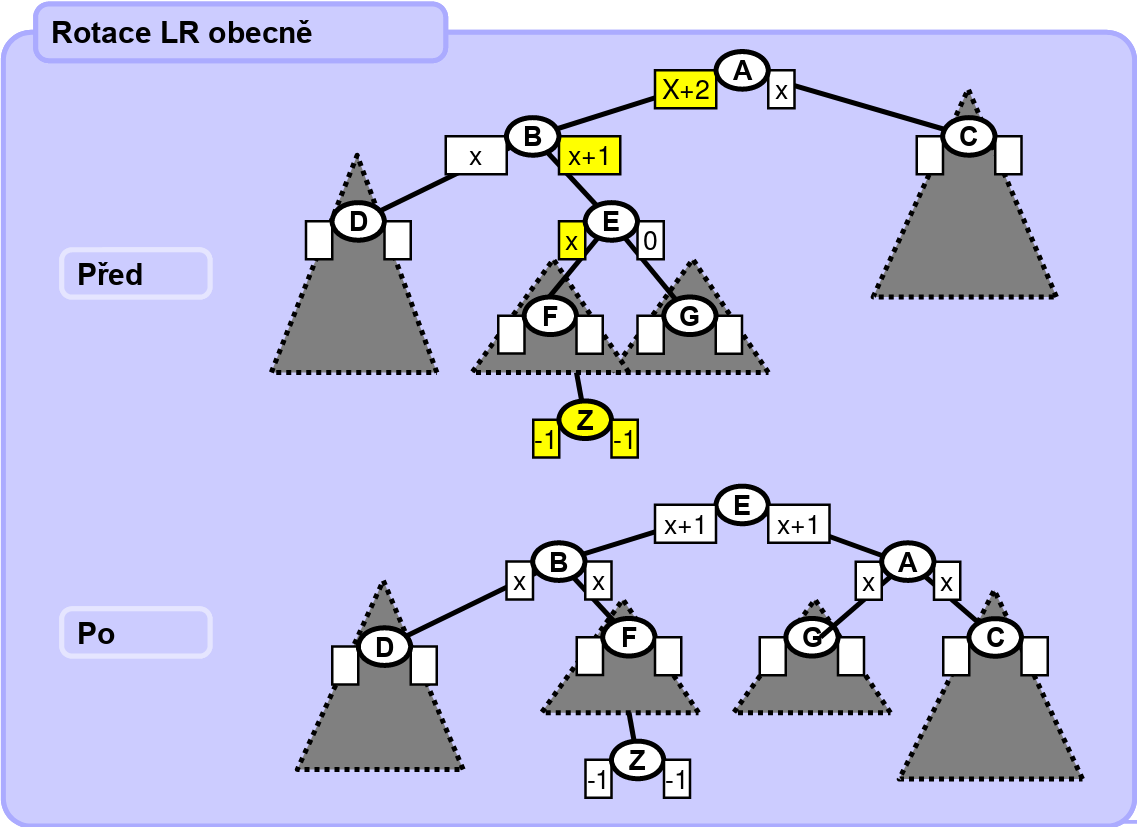
rotace_lr

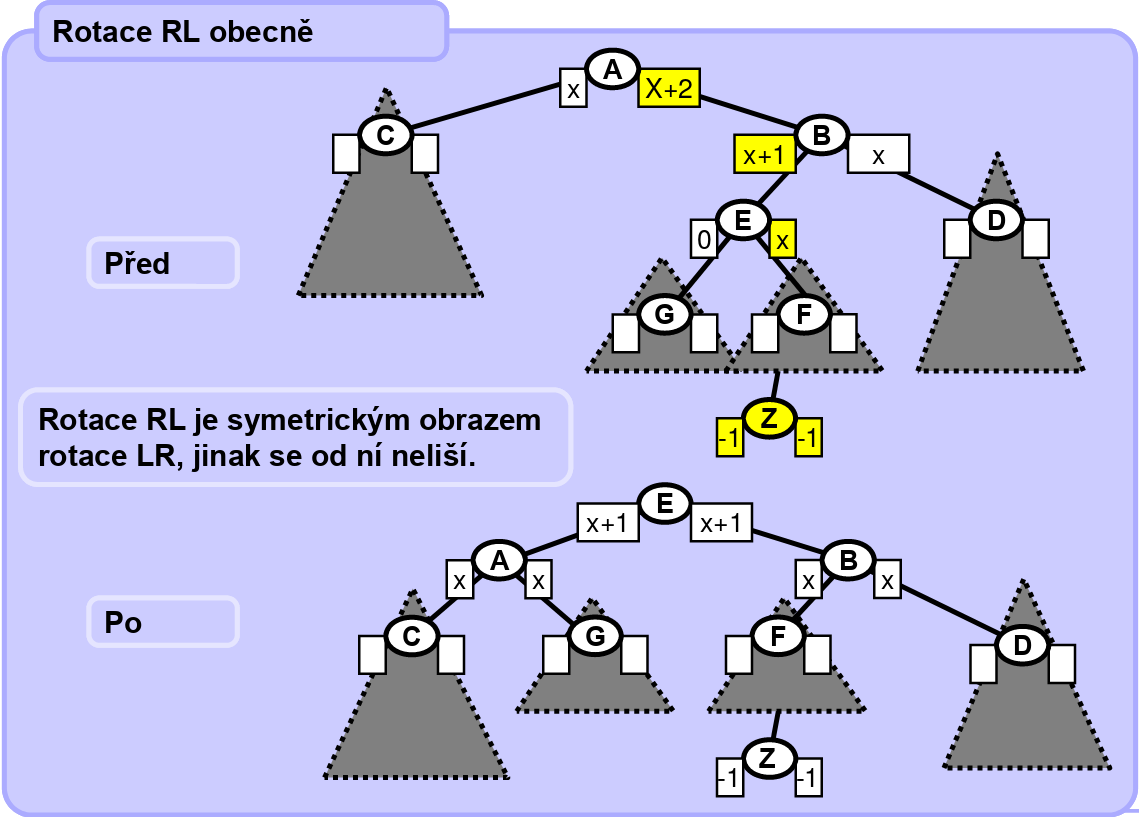
rotace_rl

Kontrolujeme takto každý uzel po cestě zpět do kořene, při vkládání i mazání. Jinak vše probíhá jako u BVS.

Vizualizace AVL s vlastním vkládáním a mazáním, včetně krokování: https://www.cs.usfca.edu/~galles/visualization/AVLtree.html

B-strom

Speciální strom, který není binární a uzly mohou obsahovat více než jeden klíč. Název také není intuitivní.

Pro B-strom řádu $k$ platí:

Listy jsou ve stejné hloubce
Všechny uzly kromě kořene obsahují maximálně $2k$ a minimálně $k$ uspořádaných klíčů
Každý uzel (kromě listů) má o 1 víc potomků, než má klíčů

Vkládání: Jakmile je uzel přeplněn, jeho $2k + 1$ klíčů se rozdělí na dvakrát $k$ klíčů a prostřední klíč (ten $+1$ ). Vytvoří se nový uzel hned vedle původního a prostřední klíč se posune o patro výš, kde se doplní napravo od původního ukazatele na uzel, a jako potomka napravo bude mít uzel s pravou polovinou klíčů co jsme rozdělili. Musíme pak zkontrolovat rodiče, protože jsme do něj přidali jeden klíč navíc, takže je možné, že pak bude třeba obsloužit přeplnění rodiče, a možná i prarodiče atd., rekurzivně směrem ke kořeni. Klíče nerotují na rozdíl od mazání.

Mazání: Jakmile je uzel příliš prázdný, jeho $k - 1$ klíčů se doplní z levého nebo pravého sourozence, “rotací” klíčů přes rodiče. Pokud mají oba $k$ prvků (případně jeden z nich neexistuje - jsme na kraji), sloučíme uzel se sousedem na jedné straně a s odpovídajícím klíčem v rodiči. Klíčů v takto vytvořeném uzlu bude $(k-1) + 1 + k$ , tedy $2k$ . Musíme pak zkontrolovat rodiče, protože jsme z něj odebrali jeden klíč.

Vizualizace B-stromu s vlastním vkládáním a mazáním, včetně krokování: https://www.cs.usfca.edu/~galles/visualization/BTree.html

Poznámka: Někdy se jako řád uvádí maximální počet potomků uzlu, protože to je obecnější (umožňuje to lichá maxima počtu klíčů v uzlu). Minimum klíčů v uzlu (mimo kořen) je pak $\left\lfloor \frac{k}{2} \right\rfloor$ .

Řešené úlohy

AVL

Řešená úloha 1: Čísla ze zadané posloupnosti postupně vkládejte do prázdného AVL vyhledávacího stromu, který podle potřeby vyvažujete.

13, 11, 10, 15, 5, 21, 8, 4, 24, 17, 6, 18, 7

Jaké se provádí rotace?

Řešení

06_1_avl

Provedli jsme rotace

R v uzlu s klíčem 13 při vložení 10
L v uzlu s klíčem 13 při vložení 21
LR v uzlu s klíčem 10 při vložení 8
RL v uzlu s klíčem 15 při vložení 18
LR v uzlu s klíčem 8 při vložení 7

Poté z něj odstraňte 13, 11, 5, 24, 17 a 18. Při mazání nahrazujte nejmenším klíčem v pravém podstromu.

Po mazání

Provedli jsme rotace

L v uzlu s klíčem 17 při odstranění 11
LR v uzlu s klíčem 21 při odstranění 24
LR v kořeni (klíč 15) při odstranění 18

Zde je strom po jednotlivých rotacích:

avl_del_1

avl_del_2

avl_del_3

Řešená úloha 2: Zdůvodněte pravdivost/nepravdivost tvrzení: Existuje AVL strom, v němž levý podstrom kořene obsahuje 4 uzly a pravý podstrom kořene obsahuje alespoň 12 uzlů.

Řešení

Takový strom existuje, například:

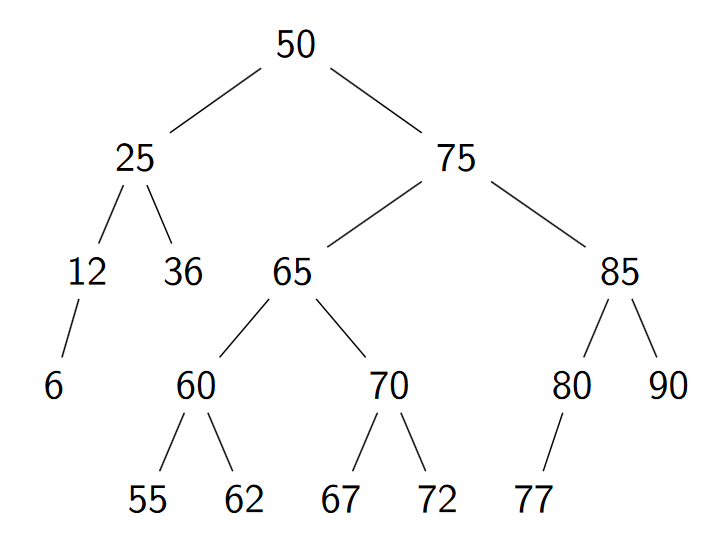
06_2_sol

B-strom

Řešená úloha 3: Vybudujte B-strom řádu 1 tak, že do nejprve prázdného stromu vložíte postupně v uvedeném pořadí následující klíče:

18, 31, 59, 20, 23, 24, 36, 60, 58, 15

Řešení

06_3

Poté v uvedeném pořadí odstraňte klíče 20, 24, 23, 36 a 60. Při mazání taktéž nahrazujte nejmenším vyšším klíčem (nejlevějším v pravém podstromu).

Po mazání

06_3_del0_1

06_3_del0_2

06_3_del1

06_3_del1_1

06_3_del2

Další úlohy

AVL

⭐ Úloha 4:

Na obrázku je uveden AVL strom. Odstraňte z něj operací delete uzly s klíči 50, 30, 25 v tomto pořadí. Rozhodněte, zda a jaké rotace budou během této úpravy použity.

Výsledek

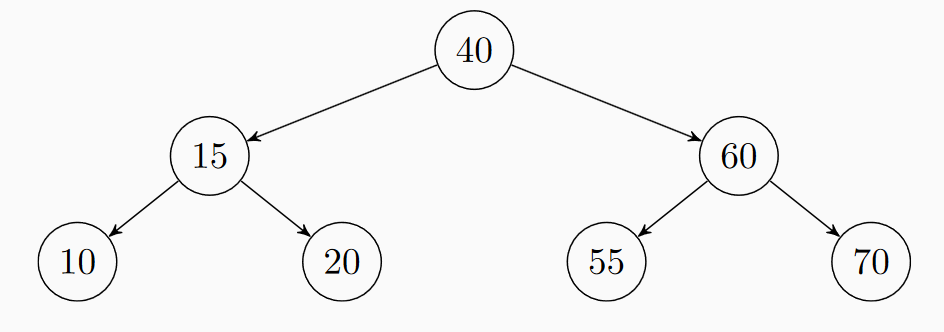
06_4_sol

⭐ Úloha 5:

Pro tentýž strom jako v zadání úlohy 4 (před mazáním) proveďte operaci insert s klíči 45, 57, 13 v tomto pořadí. Rozhodněte, zda a jaké rotace budou během této úpravy použity.

Výsledek

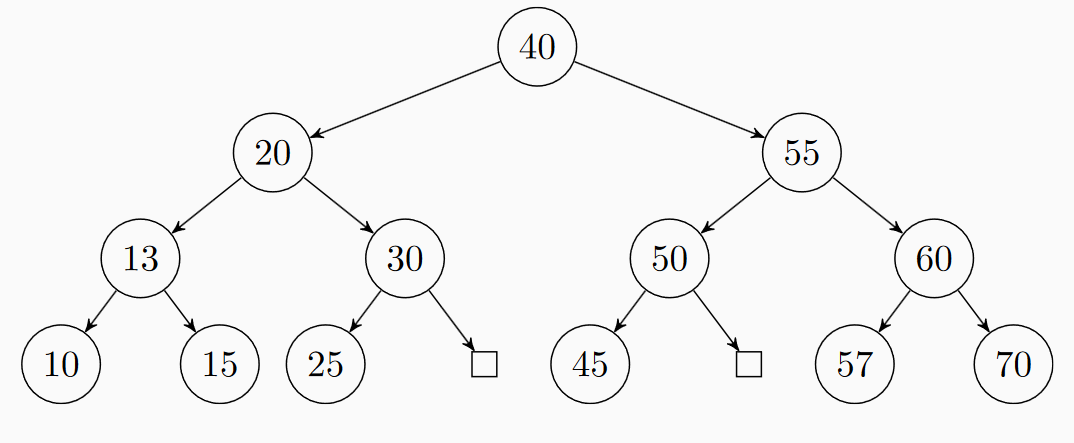
06_5_sol

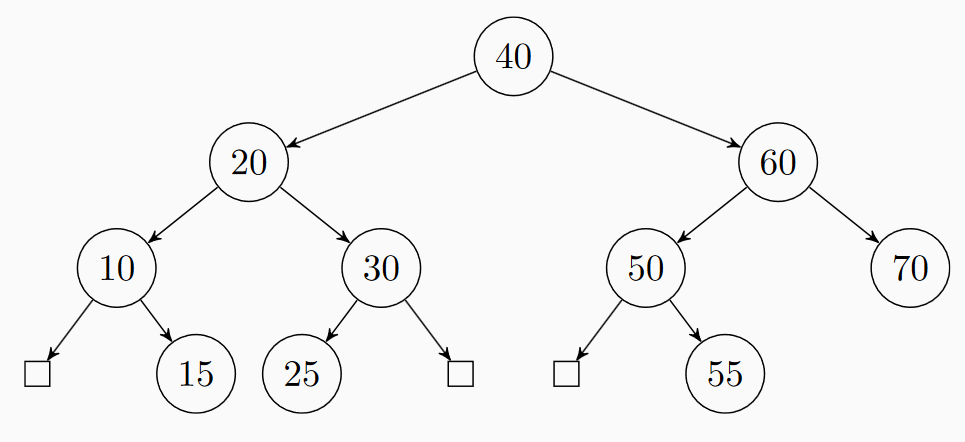
Úloha 6: Do prázdného AVL stromu postupně vkládáme klíče 23, 11, 24, 31, 17, 20, 30 a 25. Jak bude vypadat strom po vložení všech klíčů?

Výsledek

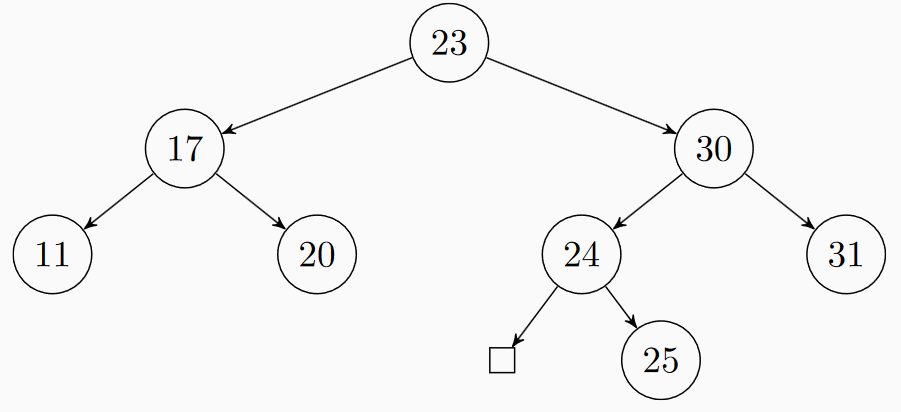
06_6_sol

Úloha 7: Do prázdného AVL stromu postupně vkládáme klíče 25, 30, 20, 17, 31, 24, 11 a 12. Jak bude vypadat strom po vložení všech klíčů?

Výsledek

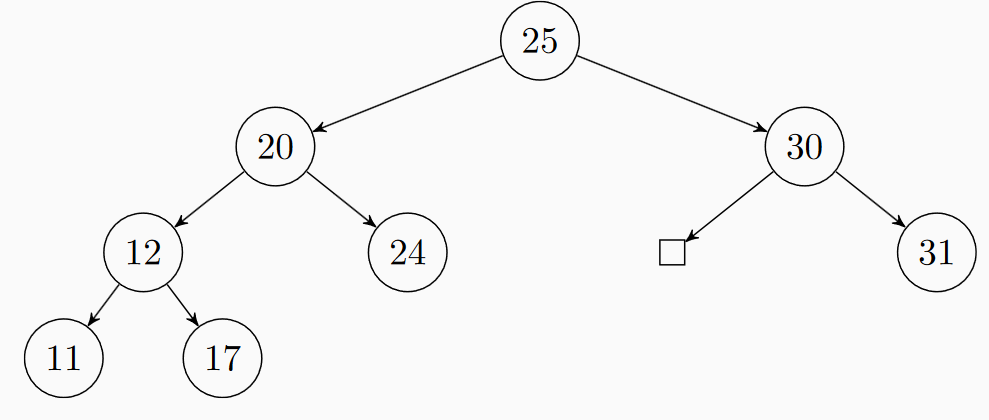
06_07_sol

⚡ Úloha 8: Jaký je minimální možný počet uzlů v AVL stromu s hloubkou 4? (Hloubka kořene je vždy 0). Nakreslete příslušný AVL strom.

Pokročilejší varianta: Jaký je minimální možný počet uzlů v AVL stromu s hloubkou D > 0?

Složitost

Úloha 9: Jednoduchá levá rotace v uzlu $u$ má operační složitost

závislou na výšce levého podstromu uzlu $u$
mezi $\textrm{O}(1)$ a $\Theta(n)$
závislou na hloubce uzlu $u$
konstantní

⭐ Úloha 10: Kolik jednoduchých rotací se maximálně provede při jedné operaci Insert v AVL stromu s n uzly?

$1$
$2$
$\log n$
$n$

⭐ Úloha 11: LR rotace v uzlu $u$ má operační složitost

závislou na hloubce uzlu $u$
$\Theta(\log n)$
konstantní
lineární

Konstrukční

Úloha 11: Nakreslete AVL strom s 8 číselnými klíči tak, aby po vložení klíče s hodnotou 19 bylo nutno provést

L rotaci v kořeni,
L rotaci v uzlu, který není kořenem,
LR rotaci v kořeni,
LR rotaci v uzlu, který není kořenem.

⭐ Úloha 12: Docent Omylný tvrdí, že vždy, když se AVL strom vyváží některou z rotací (jednoduchou nebo dvojitou) následující po smazání uzlu, sníží se tím také hloubka celého AVL stromu. Najděte k tomuto tvrzení protipříklad.

Implementační

Úloha 13: Napište proceduru strom leváRotace(strom s). Napřed si namalujte obrázek a rozmyslete si, kterých ukazatelů se změna dotkne.

Úloha 14: Předpokládejme, že každý uzel AVL stromu obsahuje reference (ukazatele, pointry) na oba své potomky a na svého rodiče (reference obsahují NIL, pokud příslušné objekty neexistují).

Určete, kolik maximálně referencí změní svou hodnotu při jednoduché pravé rotaci v takto reprezentovaném AVL stromu.
Napište funkci, která provede pravou rotaci v uzlu x. Uzel x bude parametrem funkce. Funkce vrátí ukazatel na uzel, který byl před zahájením rotace levým potomkem x.

Úloha 15: Naimplementujte metodu, která ověří, zda daný binární strom je AVL stromem.

B-strom

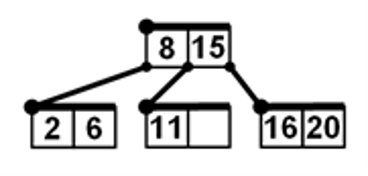
⭐ Úloha 16: Do B-stromu znázorněného na obrázku vložíme postupně klíče 14, 10.

Jak bude strom poté vypadat?

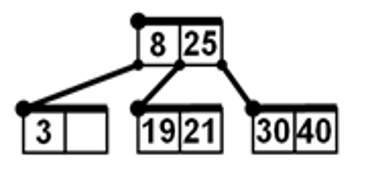
Úloha 17: Do B-stromu znázorněného na obrázku vložíme postupně klíče 7, 5.

Jak bude strom poté vypadat?

⭐ Úloha 18: Z B-stromu znázorněného na obrázku odebereme postupně klíče 4, 35. Pak bude kořen obsahovat klíč/klíče…

18
18, 28
20
20, 28
28

Odpověď

c. 20

Jak bude poté vypadat celý strom?

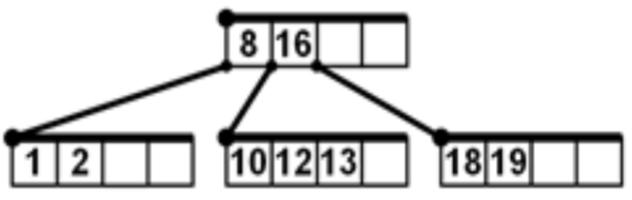
Úloha 19: Z B-stromu znázorněného na obrázku odebereme postupně klíče 18, 2. Pak bude kořen obsahovat klíč/klíče…

8
8, 16
10
10, 12
13

Jak bude poté vypadat celý strom?

Úloha 20: Klíče $1, 2, 3, 4, \ldots, 12$ v tomto pořadí vložte do prázdného B-stromu řádu 2. Jak bude vypadat výsledný strom?

Ověřte si řešení s vizualizačním programem.

⚡ Úloha 21: B-strom je řádu 10 a máme do něj umístit 100 000 klíčů. Jaká je maximální a minimální možná hloubka tohoto stromu?

Pokročilé: Jaký je maximální a minimální možný počet uzlů tohoto stromu?