7. Řazení O(n²)

7 - Řazení O(n²)

Připomenutí teorie

Přednáška 7 v oddíle Přednášky.

Selection sort

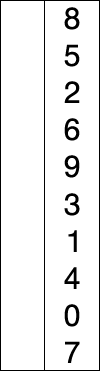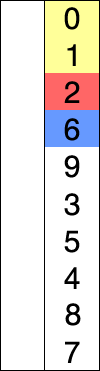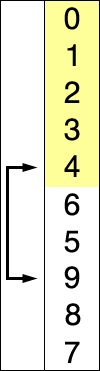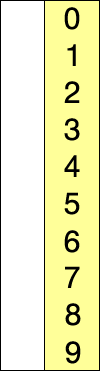
Selection sort probíhá tak, že vždy najdeme nejmenší prvek ve zbytku pole a zaměníme ho za první prvek za seřazenou částí pole.

Výhodu má pro řazení prvků, které vyžadují minimální počet přesunů.

selection_sort

Insert(ion) sort

Insert sort probíhá tak, že vždy bereme první prvek za seřazenou částí pole a postupně posouváme předchozí prvky, dokud nenajdeme prvek, který je menší (nebo nedojdeme na začátek pole). Prvek umístíme a pokračujeme dále.

Algroritmus sice provede více přesunů než Selection sort, výhodu má ale pro téměř seřazená pole, kdy nemusí dělat tolik porovnání a má tak v ideálním případě lineární složitost.

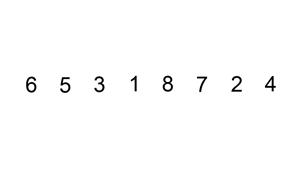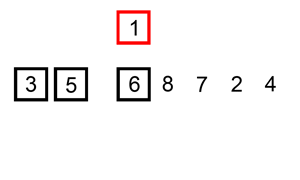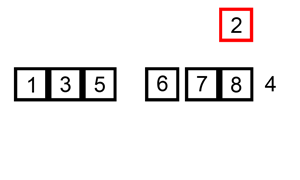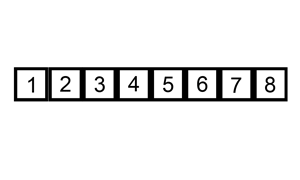
insertion_sort

Quick sort

Quick sort vybere pivota (prvek z pole) a přesune v lineárním průchodu větší prvky doprava a menší doleva. Na těchto dvou částech pole pak rekurzivně provádí to samé, dokud se nedostane k poli s jediným prvkem, které je triviálně uspořádané.

Quick sort má kvadratickou složitost jen v nejhorším případě, pokud máme neustále “smůlu” na pivoty. Jeho očekávaná složitost je $\Theta(n \log(n))$ .

quicksort

Srovnání složitostí

	Nejhorší případ	Nejlepší případ	Průměrný případ
Selection sort	$\Theta(n^2)$	$\Theta(n^2)$	$\Theta(n^2)$
Insertion sort	$\Theta(n^2)$	$\Theta(n)$	$\Theta(n^2)$
Quicksort	$\Theta(n^2)$	$\Theta(n \log(n))$	$\Theta(n \log(n))$

Nejhorší případ

Nejlepší případ

Průměrný případ

Selection sort

$\Theta(n^2)$

Insertion sort

$\Theta(n^2)$

$\Theta(n)$

$\Theta(n^2)$

Quicksort

$\Theta(n^2)$

$\Theta(n \log(n))$

Prohlédněte si vizuální animované srovnání různých řadících algoritmů.

Stabilita řazení

Řazení je stabilní, pokud prvky se stejnou hodnotou podle které řadíme zůstanou v pořadí v jakém byly v neuspořádaném poli. Toto se hodí v případě, že například máme jména seřazena podle křestních jmen a chceme je seřadit podle přijímení, přičemž chceme zachovat vzájemné uspořádání osob se stejným přijímením.

Insert sort může být stabilní, Selection sort ani Quick sort triviálně ne.

Řešené úlohy

Stabilita

Řešená úloha 1: Jak seřadí následující záznamy podle věku stabilní řadící algoritmus? Záznamy jsou ve formátu (jméno, věk).

(Franta, 32)
(Pepa, 17)
(Petr, 25)
(Jana, 23)
(David, 23)
(Martina, 25)
(Lojza, 7)
(Hanka, 23)

Řešení

(Lojza, 7)
(Pepa, 17)
(Jana, 23)
(David, 23)
(Hanka, 23)
(Petr, 25)
(Martina, 25)
(Franta, 32)

Řešená úloha 2: Zapište následující prvky do pole tak, aby Selection sort seřadil prvky nestabilně. Prvky řadíme abecedně, dolní index značí jen vzájemné pořadí stejných prvků.

$A, B, C_1, C_2, C_3, D$

Řešení

Například $C_1, D, B, C_2, A, C_3$ .

Řešená úloha 3: Níže je uveden kód Insert sortu. Představuje stabilní řazení. Jaké změny je v něm nutno provést, aby nadále korektně řadil libovolná data a přitom nebyl stabilní?

int insVal, j
for(int i = 1; i < a.length; i++) {
    insVal = a[i];
    j = i-1;
    while((j >= 0) && (a[j] > insVal)){
        a[j+1] = a[j];
        j--;
    }
    a[j+1] = insVal;
}

Řešení

V podmínce cyklu while je potřeba nahradit ostrou nerovnost > za větší nebo rovno >=.

Řazení

Řešená úloha 4: Jedenáct prvků řadíme pomocí Insert sortu. Jaký je minimální a maximální možný počet porovnání prvků během tohoto řazení? Jak pole v obou případech vypadají?

Řešení

Minimum je 10 (seřazené vzestupně) a maximum je 55 (seřazené sestupně).

Řešená úloha 5: Následující pole se řadí pomocí Quick sortu.

6, 10, 8, 5, 7, 2, 3, 9, 1, 4

Určete, jak bude pole rozděleno na “malé” a “velké” hodnoty po jednom průchodu, pokud jako pivotní hodnotu použijeme:

Řešení

pro 6: 4, 1, 3, 5, 2 | 7, 8, 9, 10, 6
pro 8: 6, 4, 1, 5, 7, 2, 3 | 9, 8, 10
pro 4: 4, 1, 3, 2 | 7, 5, 8, 9, 10, 6

Řešená úloha 6: V určitém problému je velikost zpracovávaného pole s daty rovna $2n^3 \log n$ , kde $n$ charakterizuje velikost problému. Pole se řadí pomocí

Selection sortu
Insert sortu
Quick sortu

Jaká je asymptotická složitost jednotlivých algoritmů nad uvedeným polem?

Řešení

$\Theta(n^6 log^2 n)$ pro Selection sort

$\mathrm{O}(n^6 log^2 n)$ pro Insert a Quick sort

Pro Quick sort v průměrném případě dokonce $\Theta(n^3 log^2 n)$ .

Další úlohy

Úloha 7: Jaká posloupnost vznikne, když stabilní řadicí algoritmus seřadí posloupnost $A_2 \ C_2 \ B_2 \ B_1 \ C_1 \ A_1$ , v níž platí $A_1 = A_2 < B_1 = B_2 < C_1 = C_2$ .

Odpověď

$A_2 \ A_1 \ B_2 \ B_1 \ C_2 \ C_1$

Insert sort pro speciální případy

Úloha 8:

Insert sort řadí (do neklesajícího pořadí) pole o $n$ prvcích, kde hodnoty od třetího do posledního prvku rostou a hodnoty prvních dvou prvků jsou stejné a v poli největší.

Kolik porovnání dvou prvků se provede během tohoto řazení?
Kolik celkem zápisů do řazeného pole se provede během tohoto řazení?

Řešení

Počet porovnání: $1 + 2 + 3(n-3)$ Počet zápisů: $1 + 3(n - 2)$

array

Úloha 9:

Insert sort řadí (do neklesajícího pořadí) pole o $n$ prvcích, kde hodnoty prvního a posledního prvku jsou stejné a vyšší než hodnoty ostatních prvků. Ostatní prvky mají rovněž stejnou hodnotu (ale menší než krajní prvky).

Kolik porovnání dvou prvků se provede během tohoto řazení?
Kolik celkem zápisů do řazeného pole se provede během tohoto řazení?

Řešení

Počet porovnání: $2(n - 2)$ Počet zápisů: $2(n - 2)$

array

Úloha 10: Insert sort řadí (do neklesajícího pořadí) pole o $n$ prvcích, kde v první polovině pole jsou pouze dvojky, ve druhé polovině jsou jen jedničky.

Kolik porovnání dvou prvků se provede během tohoto řazení?
Kolik celkem zápisů do řazeného pole se provede během tohoto řazení?

Složitost

Úloha 11:

Pole $n$ různých prvků je uspořádáno od druhého prvku sestupně, první prvek má nejmenší hodnotu ze všech prvků v poli. Vyberte níže všechny možnosti, které alespoň přibližně charakterizují asymptotickou složitost

Selection sortu
Insert sortu
Quick sortu

pracujícího nad tímto konkrétním polem.

a) $O(n)$

b) $\Omega(n)$

c) $\Theta(n)$

d) $O(n^2)$

e) $\Omega(n^2)$

f) $\Theta(n^2)$

Quick sort extra

⚡ Úloha 12: Quick sort řadí pole o $n$ prvcích, které nabývají pouze dvou hodnot, 1 a 2. Jedniček i dvojek je stejně mnoho, ale jejich poloha není známa. Určete, jaké je jejich
A) nejvíce příznivé,
B) nejméně příznivé
rozložení v poli.

Pro případ A) i B) určete asymptotickou složitost tohoto řazení.

⚡ Úloha 13: Předpokládejme, že vždy, když Quick sort rozdělí daný úsek pole na “malé” a “velké” hodnoty, bude jeden z těchto úseků třikrát delší než ten druhý. Určete asymptotickou složitost Quick sort-u v tomto případě.