8 - Řazení O(n log n)
Připomenutí teorie
Přednáška 8 v oddíle Přednášky. Pro implementační detaily koukněte do přednášky, zde jen popíšeme základní myšlenky.
Obecné řadící algoritmy se složitostí Θ(n log n)
Heap sort
Nejprve upravíme pole tak aby reprezentovalo haldu (heapify) - tato akce lze provést se složitostí .
Pak postupně odebíráme kořen a dáváme ho do pole za poslední prvek haldy. Toto je krát operace se složitostí . Celkem
Pokud použijeme min-heap, pole bude seřazené sestupně, pokud max-heap, bude seřazené vzestupně.
Merge sort
Přístup ve stylu “rozděl a panuj”. Algoritmus funguje tak, že rozdělíme pole na 2 díly, rekurzivně je seřadit a pak spojit (merge) dané díly v lineárním čase.
Hloubka stromu rekurzivních volání je a na každé úrovni provádíme merge na prvcích. Celkově tedy .
Merge sort je stabilní, na rozdíl od Heap sortu.
Prohlédněte si vizuální animované srovnání řadících algoritmů.
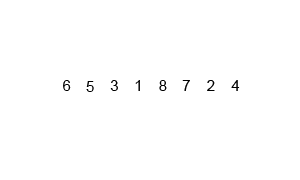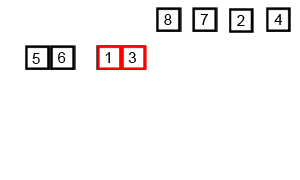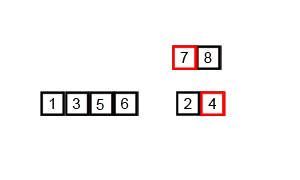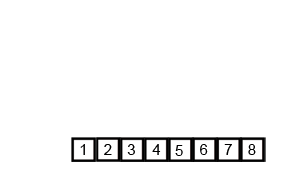
Specializované řadící algoritmy se složitostí Θ(n)
Pokud pouze porovnáváme prvky po dvojicích, není možné řadit je asymptoticky rychleji než . Proto potřebujeme jiné znalosti o datech.
Counting sort
Toto řazení je vhodné pro prvky, kde jsou duplikáty a jsme schopni enumerovat všechny prvky (typicky vhodná jsou celá čísla). Najdeme minimum a maximum, pak procházíme prvky v rozsahu hodnot a počítáme četnosti jednotlivých prvků. Poté je přesuneme prvky v novém pořadí, podle předpočítaných četností. Asymptotická složitost je kde je rozsah prvků v poli pro které počítáme četnosti.
Radix sort
Někdy nazývané přihrádkové řazení, spočívá v tom, že řadíme řetězce stejné délky nad omezenou abecedou znak po znaku. Na jednom znaku řadíme pak lineárně, podobně jako counting sort. Pro sestavení pořadí řetězců poté projdeme abecedu znak po znaku a přesouváme řetězce pro daný znak podle uloženého pořadí.
Asymptotickou složitost má radix sort kde je délka řetězců, a je počet znaků (pro zisk pořadí po každém průchodu musíme procházet všechny znaky).
Řešené úlohy
Řazení Θ(n log n)
Řešená úloha 1: Zadanou posloupnost seřaďte pomocí heap sortu. Registrujte stav v poli po každém kroku. Nejprve po každé opravě částečné haldy od prostředku pole směrem k začátku, tj. při první fázi. Potom také po každé opravě haldy a přenesení prvku z vrcholu haldy za konec haldy.
23 |
29 |
27 |
4 |
28 |
17 |
1 |
24 |
6 |
30 |
19 |
Řešení
Úprava pole na haldu - heapify. Tučně jsou projité pozice, zeleně jsou přesunuté prvky.
Polovina () pole je triviální |
23 |
29 |
27 |
4 |
28 |
17 |
1 |
24 |
6 |
30 |
19 |
Zbytek upravujeme postupně |
23 |
29 |
27 |
4 |
17 |
1 |
24 |
6 |
30 |
||
23 |
29 |
27 |
19 |
17 |
1 |
24 |
6 |
30 |
28 |
||
23 |
29 |
4 |
19 |
17 |
24 |
6 |
30 |
28 |
|||
23 |
1 |
19 |
17 |
27 |
24 |
30 |
28 |
||||
4 |
6 |
19 |
27 |
24 |
29 |
30 |
28 |
Následně odebíráme minimum a vkládáme na konec. Modře je finální pole seřazené sestupně.
1 |
4 |
17 |
6 |
19 |
23 |
27 |
24 |
29 |
30 |
28 |
4 |
6 |
17 |
24 |
19 |
23 |
27 |
28 |
29 |
30 |
|
6 |
19 |
17 |
24 |
30 |
23 |
27 |
28 |
29 |
||
17 |
19 |
23 |
24 |
30 |
29 |
27 |
28 |
|||
19 |
24 |
23 |
28 |
30 |
29 |
27 |
||||
23 |
24 |
27 |
28 |
30 |
29 |
|||||
24 |
28 |
27 |
29 |
30 |
||||||
27 |
28 |
30 |
29 |
|||||||
28 |
29 |
30 |
||||||||
29 |
30 |
|||||||||
30 |
||||||||||
Řešená úloha 2: Merge sort řadí pole šesti čísel:
8 |
1 |
7 |
6 |
4 |
2 |
Jak bude toto pole vypadat před provedením poslední operace merge?
Řešení
|
8 |
1 |
7 |
6 |
4 |
2 |
|||||||
|
8 |
1 |
7 |
6 |
4 |
2 |
|||||||
|
8 |
1 |
7 |
6 |
4 |
2 |
|||||||
|
8 |
1 |
7 |
6 |
4 |
2 |
|||||||
|
1 |
8 |
7 |
4 |
6 |
2 |
2 porovnání |
||||||
|
1 |
7 |
8 |
2 |
4 |
6 |
3 porovnání |
Nyní proběhne poslední merge.
|
1 |
2 |
4 |
6 |
7 |
8 |
4 porovnání |
Řazení Θ(n)
Řešená úloha 3: Counting sortem seřaďte pole čísel:
8 |
14 |
14 |
7 |
11 |
11 |
6 |
3 |
12 |
11 |
2 |
12 |
14 |
9 |
8 |
Řešení
Pole četností
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
1 |
1 |
0 |
0 |
1 |
1 |
2 |
1 |
0 |
3 |
2 |
0 |
3 |
Pole pozic umístění následujícího prvku
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
1 |
2 |
2 |
2 |
3 |
4 |
6 |
7 |
7 |
10 |
12 |
12 |
15 |
Nyní přesouváme prvky odzadu.
Průběh řazení:
| Index pole | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
8 |
|||||||||||||||
8 |
9 |
||||||||||||||
8 |
9 |
14 |
|||||||||||||
8 |
9 |
12 |
14 |
||||||||||||
2 |
8 |
9 |
12 |
14 |
|||||||||||
2 |
8 |
9 |
11 |
12 |
14 |
||||||||||
2 |
8 |
9 |
11 |
12 |
12 |
14 |
|||||||||
2 |
3 |
8 |
9 |
11 |
12 |
12 |
14 |
||||||||
2 |
3 |
6 |
8 |
9 |
11 |
12 |
12 |
14 |
|||||||
2 |
3 |
6 |
8 |
9 |
11 |
11 |
12 |
12 |
14 |
||||||
2 |
3 |
6 |
8 |
9 |
11 |
11 |
11 |
12 |
12 |
14 |
|||||
2 |
3 |
6 |
7 |
8 |
9 |
11 |
11 |
11 |
12 |
12 |
14 |
||||
2 |
3 |
6 |
7 |
8 |
9 |
11 |
11 |
11 |
12 |
12 |
14 |
14 |
|||
2 |
3 |
6 |
7 |
8 |
9 |
11 |
11 |
11 |
12 |
12 |
14 |
14 |
14 |
||
2 |
3 |
6 |
7 |
8 |
8 |
9 |
11 |
11 |
11 |
12 |
12 |
14 |
14 |
14 |
Řešená úloha 4: Následující posloupnost řetězců je nutno seřadit pomocí Radix Sortu (přihrádkového řazení). Proveďte všechny průchody algoritmu daným polem a zapište stavy pomocných polí po každém průchodu.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
bbc |
bac |
bcb |
aaa |
aac |
cbc |
caa |
Řešení
V každém průchodu řadíme pole podle jedné pozice, odzadu. Procházíme řetězce a vytváříme si podseznamy řetězců, které si pamatujeme pomocí polí:
-
z ukládá index prvního řetězce s daným znakem na pozici podle které řadíme
-
k ukládá index posledního řetězce s daným znakem na pozici podle které řadíme
-
d ukládá pro každý index následovníka v podseznamu řetězců (řetězec se stejným znakem na dané pozici)
Pro další iterace pak procházíme abecedu a pro každý znak bereme řetězce podle uloženého pořadí jemu příslušejících řetězců.
Po prvním průchodu:
| a | b | c | |
|---|---|---|---|
z |
3 |
2 |
0 |
k |
6 |
2 |
5 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
d |
1 |
4 |
-1 |
6 |
5 |
-1 |
-1 |
Po druhém průchodu:
| a | b | c | |
|---|---|---|---|
z |
3 |
0 |
2 |
k |
4 |
5 |
2 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
d |
5 |
4 |
-1 |
6 |
-1 |
-1 |
1 |
Po třetím průchodu:
| a | b | c | |
|---|---|---|---|
z |
3 |
1 |
6 |
k |
4 |
2 |
5 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
d |
2 |
0 |
-1 |
4 |
-1 |
-1 |
5 |
Rekonstruované seřazené pole bude tedy
| index pole | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
obsah pole |
aaa |
aac |
bac |
bbc |
bcb |
caa |
cbc |
(index původně) |
3 |
4 |
1 |
0 |
2 |
6 |
5 |
Další úlohy
Heap sort
Úloha 5: Je dána halda uložená v poli. Proveďte první krok fáze řazení v Heap sortu.
1 |
5 |
2 |
17 |
13 |
24 |
9 |
19 |
23 |
22 |
Nyní proveďte to samé pro tuto haldu:
4 |
8 |
11 |
12 |
9 |
18 |
13 |
17 |
21 |
25 |
⭐ Úloha 6: Heap sort
a) není stabilní, protože halda (heap) nemusí být pravidelným stromem
b) není stabilní, protože žádný rychlý algoritmus () nemůže být stabilní
c) je stabilní, protože halda (heap) je vyvážený strom
d) je stabilní, protože to zaručuje pravidlo haldy
e) neplatí o něm ani jedno předchozí tvrzení
Úloha 7: Vysvětlete, jak je nutno modifikovat Heap sort, aby po jeho skončení pole obsahovalo prvky seřazené vzestupně. Algoritmus musí být stejně rychlý, nejen asymptoticky, a nesmí používat žádné další datové struktury nebo proměnné.
Úloha 8: Předložíme-li Heap sort-u vzestupně seřazenou posloupnost délky , bude složitost celého řazení
a) , protože Heap sort vytvoří haldu v čase
b) , protože Heap sort vytvoří haldu v čase
c) , protože je to složitost vytvoření haldy
d) , protože je to složitost zpracování haldy
e) , protože vytvoření i zpracování haldy bude mít právě tuto složitost
Úloha 9: Dokončete implementaci Heap sortu v Pythonu.
Merge sort
Úloha 10: Merge sort řadí pole šesti čísel:
9 |
5 |
8 |
7 |
2 |
0 |
Jak bude toto pole vypadat před provedením poslední operace merge?
Úloha 11: Merge sort
a) lze napsat tak, aby nebyl stabilní
b) je stabilní, protože jeho složitost je
c) je nestabilní, protože jeho složitost je
d) je rychlý () právě proto, že je stabilní
e) neplatí o něm ani jedno předchozí tvrzení
⭐ Úloha 12: S použitím // symboliky vyjádřete asymptotickou složitost Merge sortu nad daným polem v závislosti na hodnotě . Výsledný vztah předložte v co nejjednodušší podobě.
Pole má velikost:
kde charakterizuje velikost problému.
Úloha 13: Jaká je asymptotická složitost algoritmu zvaného 4-way merge sort. Algoritmus funguje jako standardní merge sort, pouze pole rozkládá na 4 části místo dvou.
Úloha 14: Implementujte nerekurzivní variantu Merge sortu s využitím vlastního zásobníku. Vaše implementace nemusí usilovat o maximální rychlost, stačí, když dodrží asymptotickou složitost Merge sortu. Můžete využít rekruzivní implementaci Merge sortu v Pythonu.
⚡ Úloha 15: Merge Sort lze naprogramovat bez rekurze („zdola nahoru“) také tak, že nejprve sloučíme jednotlivé nejkratší možné úseky, pak sloučíme delší úseky atd. Proveďte to. Můžete využít rekruzivní implementaci Merge sortu v Pythonu.
Counting sort
Úloha 16: Counting sortem řadíme pole čísel:
50 |
88 |
87 |
87 |
93 |
87 |
23 |
53 |
70 |
89 |
53 |
62 |
Jaký bude nejmenší a největší index v poli četností?
Jaké budou pro toto pole?
56 |
54 |
20 |
13 |
44 |
75 |
84 |
39 |
31 |
34 |
68 |
Úloha 17: Řadíme 14 celých čísel. Těsně předtím, než se začne plnit výstupní pole v Counting sortu, je obsah původního pole četností následující:
| index | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|
obsah pole |
1 |
3 |
4 |
8 |
10 |
12 |
12 |
12 |
13 |
14 |
Napište, jak vypadá výsledné uspořádané pole, za předpokladu, že všechna pole začínají indexem 1.
Úloha 18: Řadíme 15 celých čísel. Těsně předtím, než se začne plnit výstupní pole v Counting sortu, je obsah původního pole četností následující:
| index | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|
obsah pole |
0 |
1 |
2 |
3 |
7 |
9 |
9 |
13 |
14 |
15 |
Napište, jak vypadá výsledné uspořádané pole, za předpokladu, že všechna pole začínají indexem 1.
⭐ Úloha 19: Uvažujme pole obsahující 1000 navzájem různých čísel v pohyblivé řádové čárce. Counting sort se pro toto pole
a) hodí, protože toto řazení má lineární složitost b) hodí, protože toto řazení má sublineární složitost c) hodí, protože čísla lze převést na řetězce d) nehodí, protože čísla v poli nemusí být celá e) nehodí, protože čísla jsou navzájem různá
Úloha 20: Na začátku Counting sortu je v poli četností uložena právě četnost výskytu každé hodnoty ve vstupním poli. V průběhu řazení se obsah pole četností průběžně mění.
Rozhodněte, zda je možno po dokončení celého řazení rekonstruovat z modifikovaného pole četností původní (a ovšem i výsledné) četnosti jednotlivých řazených hodnot.
Radix sort
Úloha 21: Následující posloupnost řetězců je nutno seřadit pomocí Radix Sortu (přihrádkového řazení). Proveďte první průchod (z celkových čtyř průchodů) algoritmu danými daty a napište, jak budou po tomto prvním průchodu seřazena.
IIYI |
PIYY |
YIII |
YPPP |
YYYI |
PYPP |
PIPI |
PPYI |
Proveďte to samé pro následující posloupnosti:
JKKJ |
KEEJ |
JKJJ |
KJKK |
KJEE |
KEEJ |
EJEE |
JEEJ |
⭐ Úloha 22: Radix sort řadí dané pole řetězců. Napište, jak budou zaplněna jednotlivá pomocná pole (z, k, d, podle přednášky) po prvním průchodu algoritmu, tj. po seřazení podle posledního znaku.
dda |
bab |
ddc |
aaa |
bcd |
dbc |
bbb |
add |
ccd |
dab |
bbc |
Jak budou zaplněna pro následující posloupnost?
dad |
caa |
cad |
aac |
bca |
dbc |
bbd |
ddc |
cda |
dac |
bbc |
⭐ Úloha 23: Radix sort právě řadí podle 3. znaku od konce a ještě průchod nedokončil. Jak se bude postupně měnit obsah polí po zařazení každého z dalších řetězců?
abbac (9), aaaaa (4), bbbac (6)
Čísla v závorkách uvádějí pozici řetězce ve vstupním poli. Aktuální obsah polí je
z1
| a | b | c |
|---|---|---|
3 |
10 |
5 |
k1
| a | b | c |
|---|---|---|
1 |
2 |
5 |
d1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
0 |
0 |
8 |
0 |
0 |
0 |
2 |
1 |
0 |
7 |
Úloha 24: Radix sort právě řadí podle 4. znaku od konce a ještě průchod nedokončil. Jak se bude postupně měnit obsah polí po zařazení každého z dalších řetězců?
baaab (11), ccaba (4), ababa (6), babab (5), bbbbc (10)
Čísla v závorkách uvádějí pozici řetězce ve vstupním poli. Aktuální obsah polí je
z1
| a | b | c |
|---|---|---|
8 |
0 |
3 |
k1
| a | b | c |
|---|---|---|
1 |
0 |
2 |
d1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|
0 |
0 |
2 |
0 |
0 |
0 |
9 |
7 |
1 |
0 |
0 |
Úloha 25: Pomocí Radix sortu řadíme pole řetězců, každý řetězec má kladnou délku k. Asymptotická složitost tohoto řazení je
a)
b)
c)
d)
e)
Úloha 26: Pole A obsahuje téměř seřazené řetězce (např. z 99% seřazené), pole B obsahuje řetězce stejné délky, ale zcela neseřazené. Radix sort seřadí asymptoticky
a) A rychleji než B
b) B rychleji než A
c) A stejně rychle jako B, použije více paměti pro řazení A
d) A stejně rychle jako B, použije více paměti pro řazení B
e) A stejně rychle jako B a použití paměti bude stejné
⚡Úloha 27: Každé kladné číslo typu int lze interpretovat jako posloupnost čtyř znaků reprezentujích jeho zápis v soustavě o základu . Jinými slovy, hodnotu každého Bytu tohoto čísla bude považovat za samostatný znak. Například číslo se rovná , takže jej lze v tomto návrhu zapsat jako , kde každé číslo interpretujeme jako samostatný symbol.
Jak je nutno modifikovat Radix sort, aby mohl řadit pole takto interpretovaných celých čísel?
Bude to časově/paměťově výhodné? Pro jak veliká pole?
Obecné
⭐Úloha 28: Kterou následující dvojici řazení je možno implementovat tak, aby byla stabilní?
a) Heap sort a Insertion sort
b) Selection sort a Quick sort
c) Insertion sort a Merge sort
d) Heap sort a Merge sort
e) Radix sort a Quick sort
⭐ Úloha 29: Poskytneme-li Quick sortu (Q) a Merge sortu (M) stejná data k seřazení, platí
a) Q bude vždy asymptoticky rychlejší než M
b) M bude vždy asymptoticky rychlejší než Q
c) někdy může být Q asymptoticky rychlejší než M
d) někdy může být M asymptoticky rychlejší než Q
e) Q i M budou vždy asymptoticky stejně rychlé