11 - Dynamické programování III
Připomenutí teorie
Přednáška 11 v oddíle Přednášky.
Optimální vyhledávací strom
Toto je úloha kde máme sestrojit BVS, pro který známe pravděpodobnosti dotazů na jednotlivé klíče. Chceme minimalizovat očekávaný počet operací, kdy nalezení klíče v hloubce vyžaduje operací. Pokud je pravděpodobnost dotazu na klíč rovna , celková cena umístění klíče do hloubky bude . Minimalizujeme součet přes všech klíčů.
Podobně jako při závorkování, optimální strom o uzlech lze vidět jako kořen a 2 optimální podstromy v levé a pravé větvi. Toto je naše “optimal substructure”. Když budeme hledat optimální strom o uzlech tak, že budeme zkoušet každý z uzlů jako kořen, budeme využívat stejné podstromy vícekrát - “overlapping subproblems”. Cenu stromu vypočteme vždy jako součet pravděpodobností výskytu všech uzlů + ceny obou podstromů.
Složitost bude také , výpočet je podobný výpočtu závorkování.
Nejdelší společná podposloupnost
V této úloze máme 2 řetězce délek a , a hledáme nejdelší podposloupnost (opět ne nutně navazující) která se vyskytuje zároveň v obou řetězcích.
Když známe nejdelší společnou podposloupnost pro kratší řetězce, můžeme toho využít pro optimální řešení pro řetězce se znakem navíc. Celé se to provádí tak, že vyplňujeme 2D pole , kde na doplňujeme čísla podle předpisu:
Toto je pak problém s tabelací, podobný těm, co jsme řešili na minulých cvičeních.
Podobný proces je používaný pro výpočet Hammingovy, či Levenshteinovy vzdálenosti dvou řetězců.
Složitost bude , protože vyplňujeme tabulku o dimenzích .
Úloha batohu (Knapsack)
Problém batohy (knapsack problem) je klasický NP-těžký problém. Máme batoh s kapacitou a předmětů, kde každý předmět má váhu/velikost a cenu/hodnotu (value) . Chceme maximalizovat hodnotu předmětů tak, aby předměty které zvolíme nepřeplnily batoh, tedy součet jejich vah byl menší než kapacita .
Uvažují se 2 varianty, 0/1 knapsack znamená, že každý předmět máme jen jeden a rozhodujeme zda ho vzít, či nevzít (0/1). Neomezená varianta pak znamená, že každý předmět můžeme vzít kolikrát chceme. Obě varianty řešíme tak, že uvažujeme optimální řešení pro batoh s menší kapacitou a do nich zkoušíme přidat další předměty.
Pro neomezený knapsack si toto lze představit převodem na hledání nejdelší cesty v DAGu s uzly a hranami s cenou předmětů mezi každými uzly které reprezentují odpovídající změnu ve zbývající kapacitě. Na obrázku vpravo je sestrojen DAG pro .
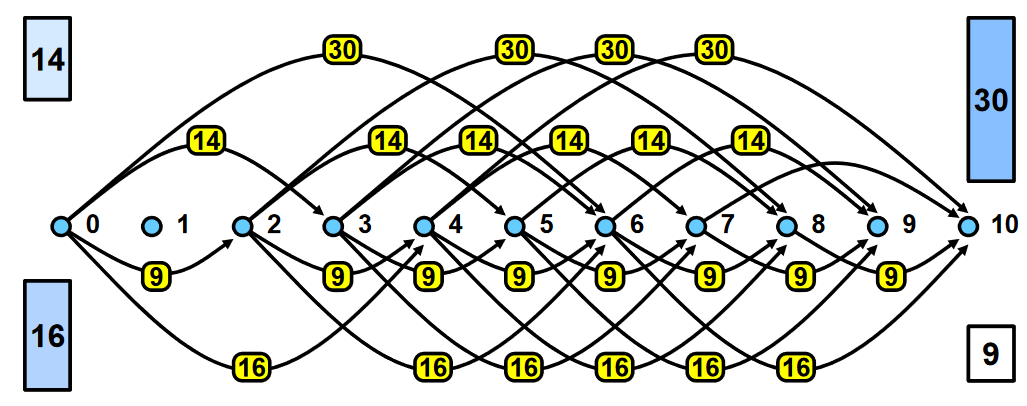
Pro 0/1 knapsack pak vyplňujeme tabulku kde řádky znamenají přidání konkrétního předmětu a sloupce jsou změny v kapacitě. Do tabulky pak zapisujeme maximální hodnotu kterou můžeme dostat s batohem dané kapacity a s danými předměty.
Knapsack je tedy převoditelný na problém nejdelší cesty v DAGu či tabelaci, což jsme již řešili na minulých cvičeních.
Řešení neomezeného i 0/1 knapsacku má složitost , protože vyplňujeme tabulku o dimenzích , či procházíme DAG s hranami.
Řešené úlohy
Optimální vyhledávací strom
Řešená úloha 1: Určete, jak bude vypadat optimální BVS, když jej vybudujeme pro 7 klíčů s frekvencemi:
-
A: 0.10
-
B: 0.10
-
C: 0.25
-
D: 0.35
-
E: 0.10
-
F: 0.05
-
G: 0.05
Řešení
Vyplňujeme od diagonály směrem doprava nahoru. Pro každou buňku projdeme páry existujících hodnot od buňky v řádku zleva a ve sloupci shora, a najdeme minimální hodnotu vypočtenou dle předpisu výpočtu výše.
- |
A |
B |
C |
D |
E |
F |
G |
|
A |
0 |
0.10 |
0.30 |
0.75 |
1.45 |
1.75 |
1.90 |
2.10 |
B |
- |
0 |
0.10 |
0.45 |
1.15 |
1.35 |
1.50 |
1.70 |
C |
- |
- |
0 |
0.25 |
0.85 |
1.05 |
1.20 |
1.40 |
D |
- |
- |
- |
0 |
0.35 |
0.55 |
0.70 |
0.90 |
E |
- |
- |
- |
- |
0 |
0.10 |
0.20 |
0.35 |
F |
- |
- |
- |
- |
- |
0 |
0.05 |
0.15 |
G |
- |
- |
- |
- |
- |
- |
0 |
0.05 |
- |
- |
- |
- |
- |
- |
- |
- |
0 |
Diagonála obsahuje nuly, které reprezentují prázdné stromy.
Strom lze rekonstruovat, pokud si zapamatujeme např. který index v řádku jsme využili pro výpočet minimální hodnoty v buňce. To nám zároveň přesně určí i pozici ve sloupci. Když pak konstruujeme (pod)strom, kořen bude vždy klíč na pozici kde je index zapsaný v buňce.
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
- |
A |
B |
C |
D |
E |
F |
G |
|
A |
1 |
3 |
3 |
4 |
||||
B |
- |
3 |
4 |
4 |
4 |
4 |
||
C |
- |
- |
3 |
4 |
4 |
4 |
4 |
|
D |
- |
- |
- |
4 |
4 |
4 |
4 |
|
E |
- |
- |
- |
- |
5 |
|||
F |
- |
- |
- |
- |
- |
6 |
7 |
|
G |
- |
- |
- |
- |
- |
- |
||
- |
- |
- |
- |
- |
- |
- |
- |

Nejdelší společná podposloupnost
Řešená úloha 2: Najděte nejdelší společnou podposloupnost dvojice řetězců:
-
11101001000
-
00010010111
Řešení
Doplněním tabulky dle předpisu výše:
- |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
- |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
||
0 |
0 |
0 |
0 |
0 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
2 |
3 |
3 |
3 |
3 |
|
1 |
0 |
1 |
1 |
1 |
1 |
2 |
2 |
3 |
4 |
4 |
4 |
|
0 |
0 |
1 |
1 |
1 |
2 |
2 |
3 |
3 |
4 |
5 |
5 |
|
0 |
0 |
1 |
1 |
1 |
2 |
2 |
3 |
4 |
4 |
5 |
6 |
|
1 |
0 |
1 |
2 |
2 |
2 |
3 |
3 |
4 |
5 |
5 |
6 |
|
0 |
0 |
1 |
2 |
2 |
3 |
3 |
4 |
4 |
5 |
6 |
6 |
|
1 |
0 |
1 |
2 |
3 |
3 |
4 |
4 |
4 |
5 |
6 |
6 |
|
1 |
0 |
1 |
2 |
3 |
3 |
4 |
4 |
4 |
5 |
6 |
6 |
|
1 |
0 |
1 |
2 |
3 |
3 |
4 |
4 |
4 |
5 |
6 |
6 |
Jde o podposloupnost 0001000, což lze vyčíst zpětně z diagonálních přechodů v tabulce výše. (Viz modrá “trasa”)
Úloha batohu (Knapsack)
Řešená úloha 3: Řešte neomezenou variantu úlohy batohu pro kapacitu 10 a tři předměty, jejichž váhy jsou postupně 1, 3, 6 a ceny jsou ve stejném pořadí předmětů 11, 33, 65.
Jaká bude maximální cena předmětů v batohu?
Převodem na DAG
Nalezením nejdelší (dle ohodnocení hran) cesty v tomto DAGu.
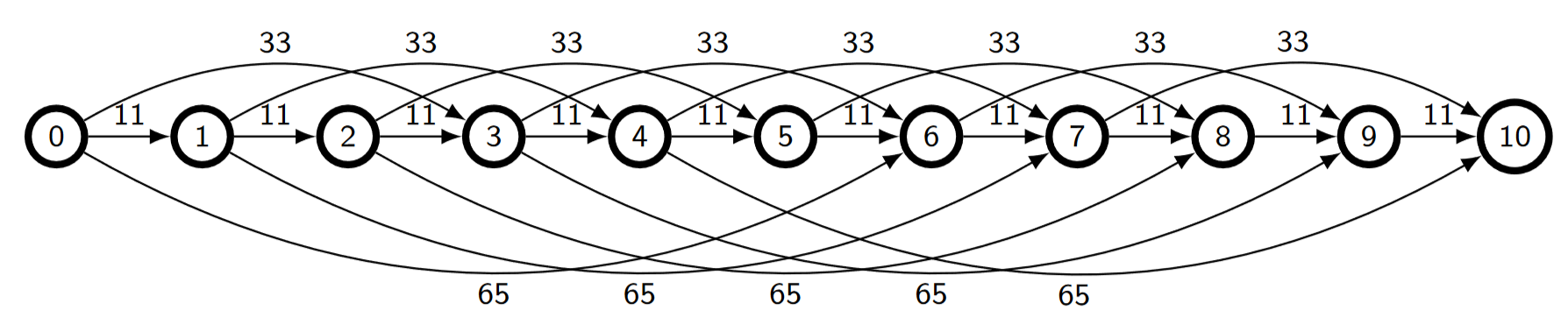
Tabulkou
Pro každou buňku se zkusím pro každý předmět podívat na hodnotu na indexu nižším o váhu předmětu. K té hodnotě přičtu cenu předmětu a z těchto čísel vyberu maximum a vložím do buňky.
Zaplněná kapacita |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Nejlepší cena |
0 |
11 |
22 |
33 |
44 |
55 |
66 |
77 |
88 |
99 |
110 |
Index právě přidaného předmětu |
0 |
1 |
1 |
2 |
1 |
1 |
2 |
1 |
1 |
2 |
1 |
Indexujeme předměty od 1.
Jaké bude řešení pro 0/1 knapsack pro stejné předměty a kapacitu 7?
Řešení
Za každou řádku přidávám jeden předmět. Přičítám k předchozí řádce, s posunem dle váhy předmětu.
Zaplněná kapacita |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Žádný předmět |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Předmět 1 |
0 |
11 |
11 |
11 |
11 |
11 |
11 |
11 |
Předměty 1-2 |
0 |
11 |
11 |
33 |
44 |
44 |
44 |
44 |
Předměty 1-3 |
0 |
11 |
11 |
33 |
44 |
44 |
65 |
76 |
Obsah batohu lze rekonstruovat z tabulky takto:
-
začneme vpravo dole,
-
posuneme se doleva dokud bychom nesnížili cenu batohu (hodnotu v buňce) - toto je “volná” kapacita
-
pokud je v buňce o 1 výš stejné číslo:
-
předmět z řádky nepřidáme a posuneme se o řádek výš do stejného sloupce
-
pokud ne, předmět přidáme a posuneme se o řádek výš, s posunem dle váhy přidaného předmětu
-
-
opakujeme proces od bodu 2
Další úlohy
Optimální vyhledávací strom
⭐ Úloha 4: Pravděpodobnost dotazu na jednotlivé klíče v obou daných BVS je tato:
A: 0.10 B: 0.20 C: 0.25 D: 0.05 E: 0.10 F: 0.25 G: 0.05
Vypočtěte, který strom je výhodnější pro operaci FIND.
Úloha 5: Určete, jak bude vypadat optimální BVS, když jej vybudujeme pro 7 klíčů s frekvencemi:
E: 0.04 F: 0.05 G: 0.22 H: 0.04 I: 0.06 J: 0.05 K: 0.15
Nejdelší společná podposloupnost
⭐ Úloha 6: Najděte nejdelší společnou podposloupnost dvojice řetězců
-
1100110011001100
-
1010101010101010
Úloha 7: Najděte nejdelší společnou podposloupnost dvojice řetězců
-
110100100010000100001000001
-
001011011101111011110111110 = doplněk
Úloha batohu (Knapsack)
⭐ Úloha 8: Řešte 0/1 variantu úlohy batohu pro kapacitu 130 a pět předmětů, jejichž váhy jsou postupně 20, 30, 40, 50, 60 a ceny jsou ve stejném pořadí předmětů 11, 33, 45, 58, 65.
Jaká bude maximální cena předmětů v batohu?
Uvažte, jak se vyhnout tabulce se cca 130 sloupci a upravte postup řešení tak, aby stačilo řádově méně sloupců.
Ostatní úlohy
⚡ Úloha 9: Každá zásilka ve skladu má určenou váhu a je nutno všechy zásilky naložit na dvě přistavené dodávky tak, aby se váhy nákladů na obou dodávkách lišily co nejméně.
Zdůvodněte, zda lze či nelze metodu DP pro řešení úlohy batohu využít i v této situaci.
Úloha 10: Kryštof staví malé sportovní lodě. Vyrábí jich několik typů a vždy se věnuje stavbě jen jedné lodě, dokud není hotová. Pro každý typ lodě zná počet dní potřebný ke stavbě lodě a zná svůj zisk z jejího prodeje. Ví, kolik dní bude letos v sezóně věnovat své práci.
Navrhněte metodu dynamického programování, která bude maximalizovat Kryštofův výdělek za letošní sezónu.